Представьте, что на заводе производство работает круглосуточно. Продукция складывается прямо на склад. Порядок ввода и вывода поступает случайным образом. Ввод всегда постоянный, а вывод только в дневное время. Поскольку общее содержимое хранилища должно оставаться постоянным, это означает, что в то время, когда выполняется вывод (дневное время), помимо циклов ввода, должно выполняться относительно большее количество перемещений вывода. Дневное время является «часом пик» хранилища, потому что большинство перемещений приходится совершать в дневное время. В дневное время вероятность выхода вдвое больше вероятности входа. Так что вы можете сравнить это с игрой в кости. Треть чисел на кубиках окрашена в красный цвет, и тогда красный цвет будет означать, что происходит ввод. Две трети чисел на кубиках окрашены в синий цвет, и синий тогда будет означать, что происходит выход.






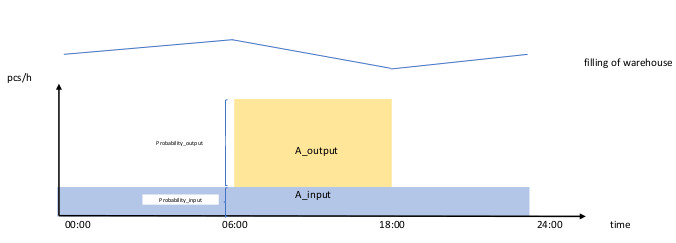
На рисунке верхняя зигзагообразная линия указывает на заполнение хранилища. Когда линия поднимается, хранилище заполняется, а когда оно опускается, хранилище опустошается. Поскольку заполнение хранилища происходит медленнее, наклон вверх вдвое превышает наклон вниз. На нижнем графике скорость наполнения в шт. / Час отмечена на оси времени. Вход (синий) в хранилище непрерывен по оси времени (x), потому что фабрика работает круглосуточно. Ось ординат отмечает количество штук в час, поступающих на склад. Светло-красная область - выход из хранилища в дневное время. Таким образом, если содержимое хранилища является постоянным в течение нескольких дней, Area_output (= выходных шт. / Час, умноженных на 12 часов) должен быть равен Area_input (ввод - шт. / Час, умноженный на 24 часа). и это означает, что в течение дня вероятность выхода (2/3) в два раза больше вероятности входа (1/3).
Рабочий может выполнять 3 разных типа движений: 1.) цикл ввода 2.) цикл вывода 3.) комбинированный цикл Комбинированные средства: вводить предмет, а сразу после вынимать предмет из хранилища одним движением. Комбинированный цикл быстрее, чем простое добавление цикла ввода и вывода, поскольку в нем задействовано меньше отключений. (Это в основном то, что жена говорит своему мужу: «Когда ты ходишь по магазинам, не могли бы вы вынести мусор одновременно»). Поэтому важно учитывать положительное влияние комбинированного цикла на пропускную способность хранилища. Для расчета возможной пропускной способности хранилища важно время цикла для всех входных, выходных и комбинированных циклов. В приведенной выше игре с бросанием кубиков это будет означать: «когда у нас есть случай, когда красное число следует за синим числом», и в этом случае это будет «удача» (или лучше: экономия времени ) сочетание. Тогда возникает вопрос, сколько циклов ввода и вывода можно комбинировать, чтобы максимально использовать преимущества комбинированного цикла.
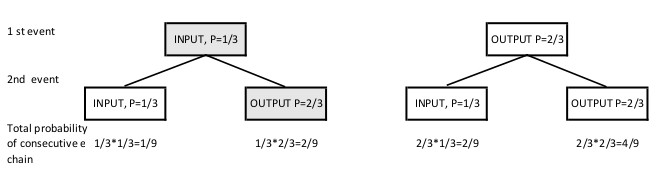
Какова вероятность того, что рабочий сможет совершить комбинированное движение? начиная с самого простого случая, что есть только два последовательных движения. Таким образом, первое движение может быть либо входом (вероятность 1/3), либо выходом (вероятность 2/3). После первого движения вероятность следующего движения точно такая же (1/3 против 2/3), как и раньше. Итак, мы имеем 4 различных комбинации движений, и каждая из этих последовательных цепочек событий имеет разную вероятность. Однако в сумме вероятность составляет 1/9 + 2/9 + 2/9 + 4/9 = 1. Но это число не дает отдельного комбинированного цикла, а также, не учитывается, что комбинированный цикл сократил общее количество шагов.
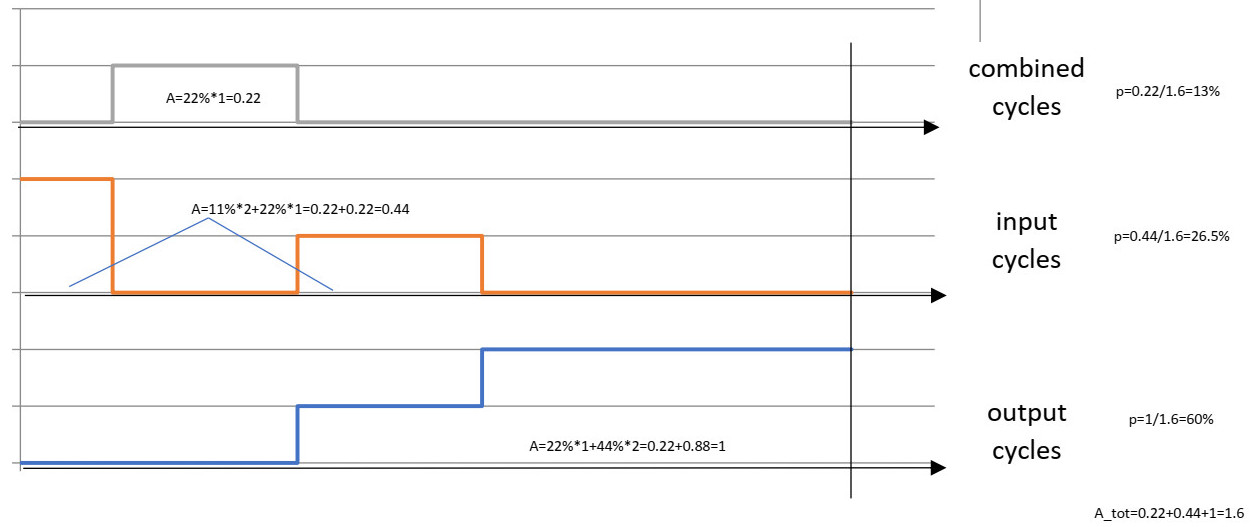
На диаграмме показана древовидная диаграмма, но сделанная в масштабе, но по оси абсцисс отложена доля вероятности каждого хода событий в масштабе. Самая низкая синяя кривая представляет собой масштаб выходных движений. Итак, то, что показано на «древовидной» диаграмме в виде правой ветви, - это ход событий с первым событием как выходом (p = 2/3), а затем как входом (p = 1/3) с общей вероятностью 2/9. = 22%, что теперь является первой ступенью (высота ступени равна 1, потому что мы говорим об одном выходном событии) на кривой лестницы с всего двумя ступенями с шириной ступеньки 22%. А внешняя правая-правая ветвь верхней «древовидной» кривой является следующим шагом синей кривой, и ее ширина составляет 44% (= 2/3 * 2/3 = 4/9). А высота ступеньки 2, потому что у нас 2 выходных события. Точно так же красная кривая показывает вероятность входного цикла, но в масштабе. Самая крутая часть находится на левой стороне, и она представляет собой внешнюю левую ветвь схемы дерева выше, с вероятностью 1/3 * 1/3 = 1/9 (11%), что в таком случае является шириной первого ступенька нисходящей светло-красной кривой лестницы. Высота этого шага равна 2, потому что это два входных движения вместе. В середине еще один кирпич, шириной 1/3 * 2/3 = 33% и высотой 1. Верхняя серая кривая показывает часть комбинированного цикла, которая отмечена серым цветом на древовидной диаграмме. Ширина (синоним вероятности) составляет 1/3 * 2/3 = 2/9 = 22%, а высота равна 1, так как у нас только одно событие. Если бы у нас не было «синергетического» эффекта комбинированного цикла, высота этого блока должна была бы быть 2, но поскольку у нас есть только одно движение, высота этого блока равна только 1. Область под каждой из этих трех разных кривых представляет вероятность соответствующего события. Таким образом, площадь кривой выходного цикла составляет 0,22 * 1 + 0,44 * 2 = 0,22 + 0,88 = 1. Площадь под кривой ввода составляет 0,11 * 2 + 0,22 * 1 = 0,44, а площадь под кривой комбинированного цикла составляет 0,22 * 1 = 0,22. Площадь под всеми тремя кривыми вместе должна быть 1 (100%), так как она не может быть больше. А вероятность цикла выпуска - это отношение площади под кривой выпуска к общей площади под всеми тремя кривыми. Таким образом, площадь под кривой выпуска равна 1, а площадь под всеми кривыми вместе составляет 0,22 + 0,44 + 1 = 1,6, поэтому относительная вероятность цикла выпуска составляет 1 / 1,6 = 0,6 (60% вероятность цикла выпуска). Соответственно, отношение площади под кривой ввода к общей площади составляет 0,44 / 1,6 = 0,265 (что означает вероятность 26,5% для цикла ввода) А вероятность комбинированного цикла составляет 0,2271,6 = 0,13 (13%). Сумма всех вероятностей должна составлять 100% = 13,5% + 26,5% + 60% = 100%.
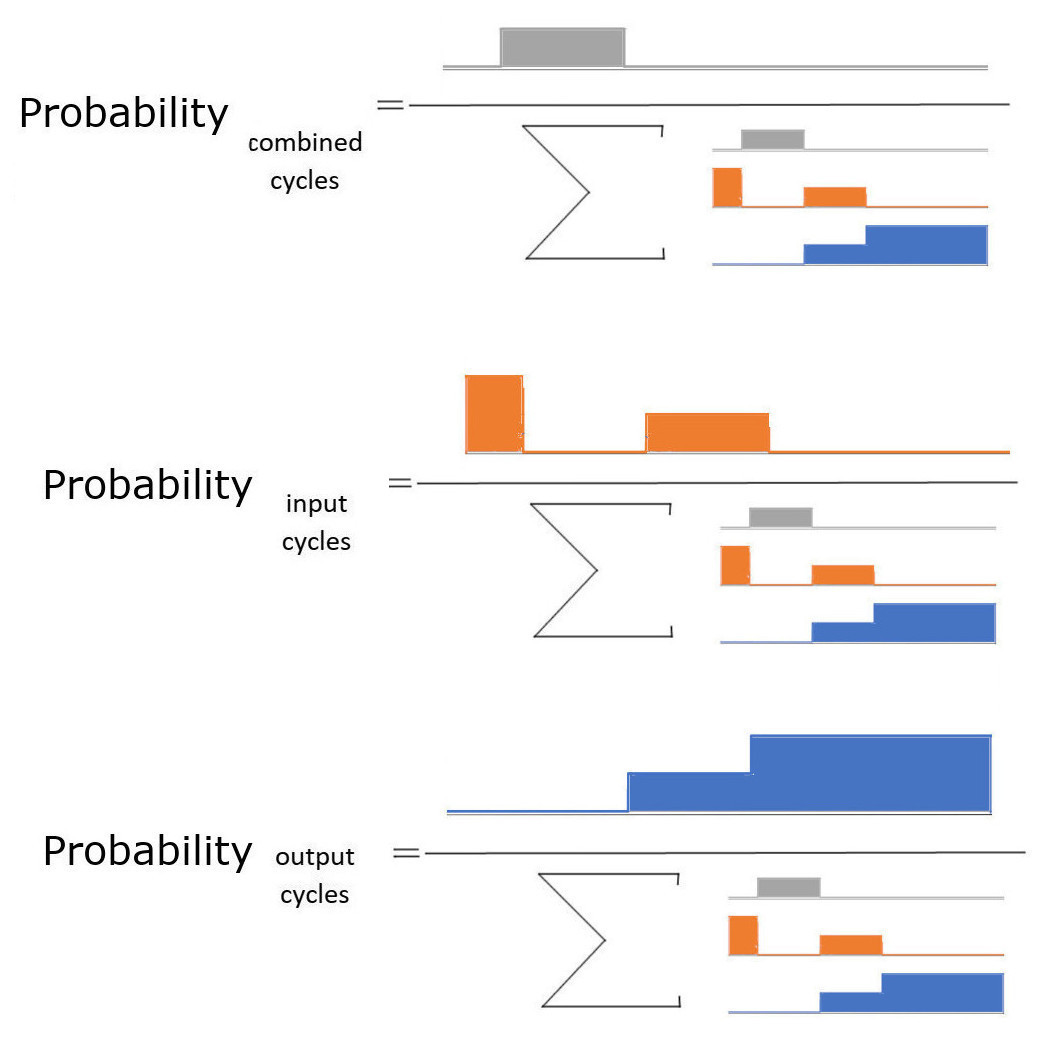
> Вероятность различных событий (комбинированных, входных, выходных) - это область соответствующего события. делится на площадь всех событий вместе.

Следующим шагом в рассмотрении является добавление еще одного шага, чтобы у нас было 3 последовательных события. Комбинированный цикл теперь появляется трижды в общем количестве восьми различных возможных событий. Таким образом, в зависимости от количества последовательных событий, вероятность всегда равна 2 в квадрате количества событий. Соответственно, цепочка из 3 последовательных входных событий составляет 1/3 * 1/3 * 1/3 = 1/27 0,037 = 3,7%, что не является большим числом.
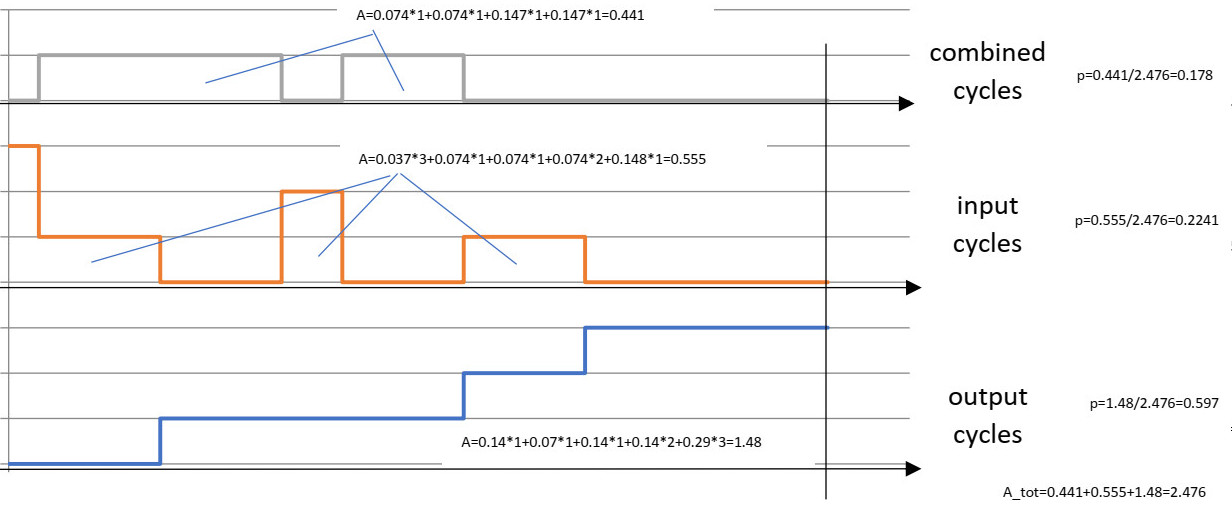
Таким образом, при трех последовательных событиях вероятность комбинированного цикла составляет 18%, вероятность входного цикла составляет 22%, а вероятность выходного цикла составляет 60%, а сумма всех вероятностей, конечно, составляет 100%. Мы также можем видеть, что наша "лестничная кривая" имеет на одну ступень больше, всего три ступени, но кривая комбинированного цикла имеет только одну ступень.
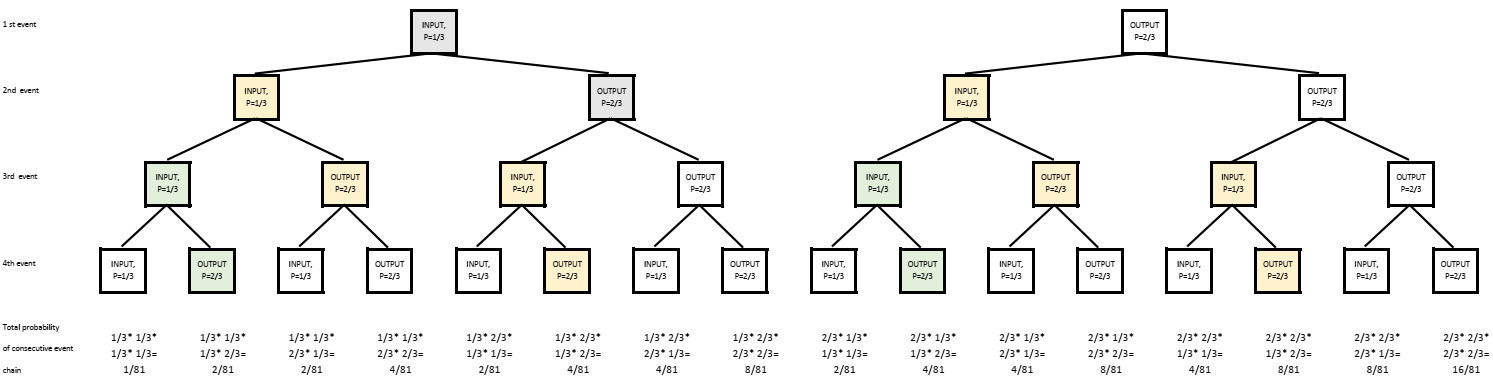
Поскольку теперь у нас есть рутина с этой процедурой, и мы становимся все более и более любопытными, мы можем продолжить делать древовидную диаграмму даже с четырьмя последовательными шагами.
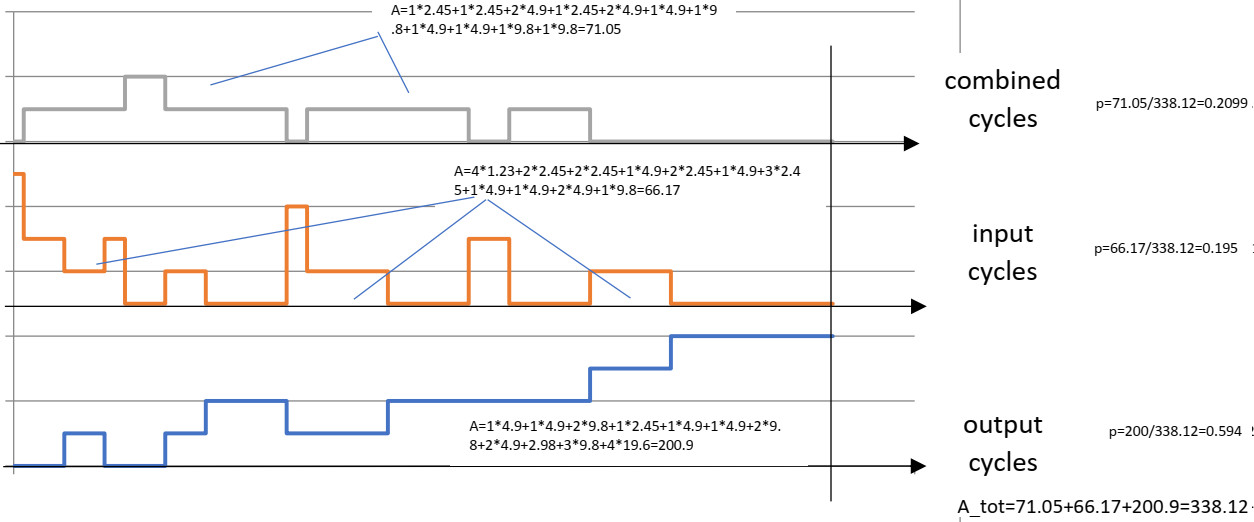
К сожалению, существует проблема с пространством в направлении ширины бумаги, кажется, невозможно уместить еще больше ветвей в эту древовидную диаграмму. Но вероятностная схема может быть продолжена, хотя ширина шага становится все меньше и меньше. Он дает количественный обзор того, сколько комбинированных циклов может быть достигнуто по сравнению с циклом ввода и вывода, поскольку сравниваются области под тремя разными кривыми.
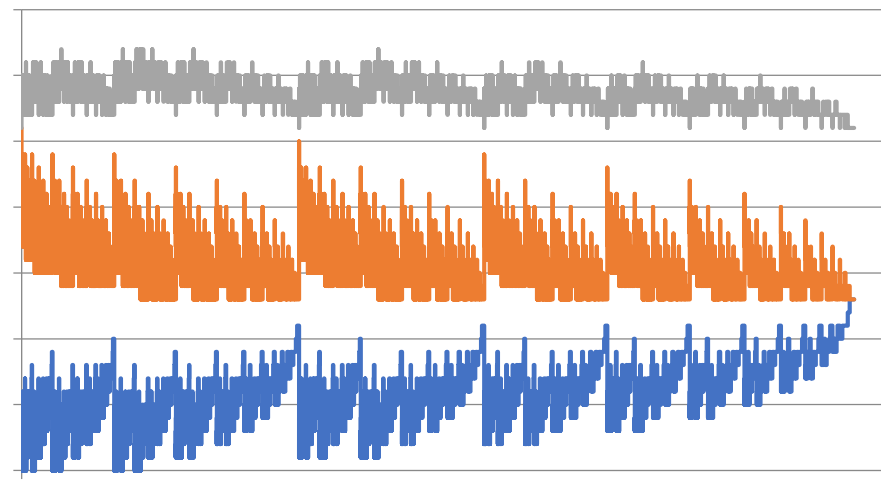
При продолжении увеличения количества событий вероятность комбинированного цикла приближается к 26%, вероятность входного цикла составляет 16%, а вероятность выходного цикла достигает примерно 58%.
До сих пор все мысли основывались на предположении, что фабрика работает 24 часа в сутки, а производительность в дневное время составляет 12 часов в сутки. Другой вопрос, как будет выглядеть ситуация, когда дневное время будет 16 часов, что соответствует дню с тремя сменами, когда две смены можно использовать для погрузочных работ. Возможно ли, что, если загрузка будет производиться даже 24 часа в сутки, все циклы могут быть выполнены в комбинированном режиме?
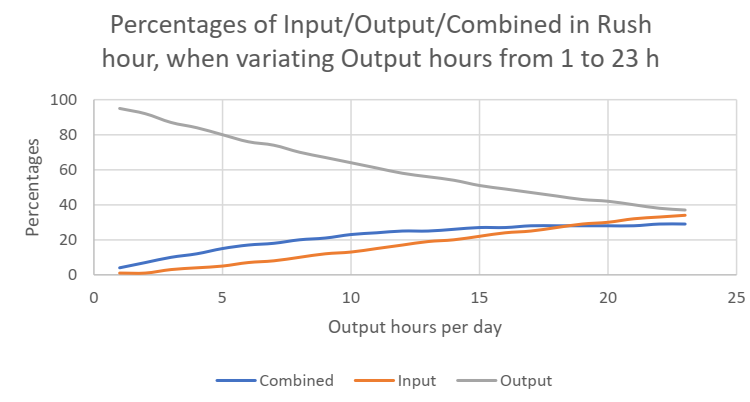
Эта кривая, на которой время выхода в дневное время меняется, немного теоретически, потому что она также показывает нереалистичную ситуацию, которая, например, когда очень мало выходных часов в день (скажем, только 1 час) означает, что в час пик почти все движения должны быть выходными движениями, поэтому никакие комбинации невозможны, а также невозможен ввод. Но это довольно нереальный сценарий. На другом конце кривой пропорции различных движений (входных, выходных и комбинированных) довольно равны, почти как 1/3 - 1/3 - 1/3. Но, в отличие от ожидаемого, комбинированный цикл никогда нельзя полностью использовать, очевидно, из-за стохастической природы процесса, когда невозможно предсказать или контролировать, какое из различных движений произойдет дальше.
Для расчета приведенных диаграмм использовалась программа с листингом на языке Python.