Sannolikhetsspel i lagring

Föreställ dig att det finns en fabrik där produktionen körs 24 timmar om dygnet. Produkterna lagras i ett lager. In- och utgångsordrar kommer in slumpmässigt. Ingången är alltid konstant men utgången sker endast under dagtid. Eftersom lagringsinnehållet måste förbli konstant innebär detta att under den tidsperiod då lagringsutgången utförs (dagtid) måste relativt fler utgångsrörelser utföras jämfört med inmatningscyklerna. Dagtid är lagrets "rusningstid" eftersom de flesta rörelser måste göras under dagtid. Under dagtid är sannolikheten för utgång dubbelt så stor som sannolikheten för inmatning. Så du kan jämföra det med ett tärningsspel. En tredjedel av siffrorna på tärningarna är målade röda och sedan kommer rött att indikera att inmatning sker. Två tredjedelar av siffrorna på tärningarna är målade blå och sedan kommer blått att indikera att utgång sker.

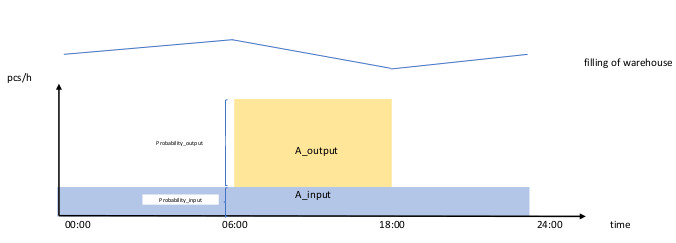
I bilden indikerar den översta zigzaglinjen lagringsfyllningen. När linjen går upp fylls lagret och när den går ner töms lagret. Eftersom lagringsfyllningen är långsammare är lutningen uppåt dubbelt så stor som lutningen nedåt. I diagrammet nedan är fyllningshastigheten i st./tim markerad på tidsaxeln. Ingången (blå) till lagret är kontinuerlig på tidsaxeln (x) eftersom fabriken körs dygnet runt. Y-axeln markerar antalet delar per timme som kommer in i lagret. Det ljusröda området är utgången från lagret under dagtid. Så om lagringsinnehållet är konstant under flera dagar eller veckor måste Area_output (= utgångsst./tim multiplicerat med 12 timmar) vara lika med Area_input (ingångsst./tim multiplicerat med 24 timmar). och detta innebär att under dagen är sannolikheten för utgång (2/3) dubbelt så stor som sannolikheten för inmatning (1/3).

En arbetare kan utföra 3 olika typer av rörelser: 1.) inmatningscykel 2.) utgångscykel 3.) kombinerad cykel Kombinerade medel: mata in ett objekt och ta sedan omedelbart ut ett objekt från lagret i en enda rörelse. Den kombinerade cykeln är snabbare än att helt enkelt lägga till inmatnings- och utgångscykeln eftersom färre nedtider är involverade. Därför är det viktigt att ta hänsyn till den positiva effekten av den kombinerade cykeln på lagrets genomströmning. För cykeltiden för alla inmatnings-, utgångs- och kombinerade cykler är det viktigt för beräkningen av lagrets möjliga genomströmning. I tärningsspelet ovan skulle detta innebära: "när vi har ett fall där en blå siffra följs av en röd siffra", och i så fall skulle detta vara "tur" (eller bättre: tidsbesparing) av kombinationen. Då uppstår frågan, hur många inmatnings- och utgångscykler kan kombineras för att maximera fördelarna med den kombinerade cykeln.

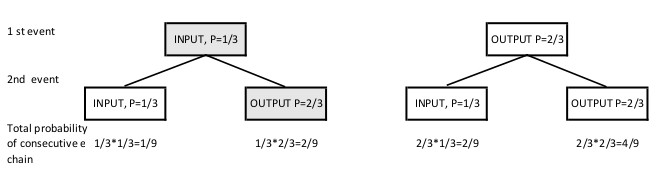
Vad är sannolikheten för att arbetaren kan utföra en kombinerad rörelse? Börja med det enklaste fallet, att det bara finns två på varandra följande rörelser. Så den första rörelsen kan vara antingen en inmatning (sannolikhet 1/3) eller en utgång (sannolikhet 2/3). Efter den första rörelsen är sannolikheten för nästa rörelse exakt densamma (1/3 mot 2/3) som tidigare. Så vi har 4 olika kombinationer av rörelser, och varje kedja av på varandra följande händelser har en annan sannolikhet . Men den totala sannolikheten är 1/9 + 2/9 + 2/9 + 4/9 = 1. Men detta nummer ger inte en separat kombinerad cykel, och det beaktas inte att den kombinerade cykeln minskade det totala antalet steg.

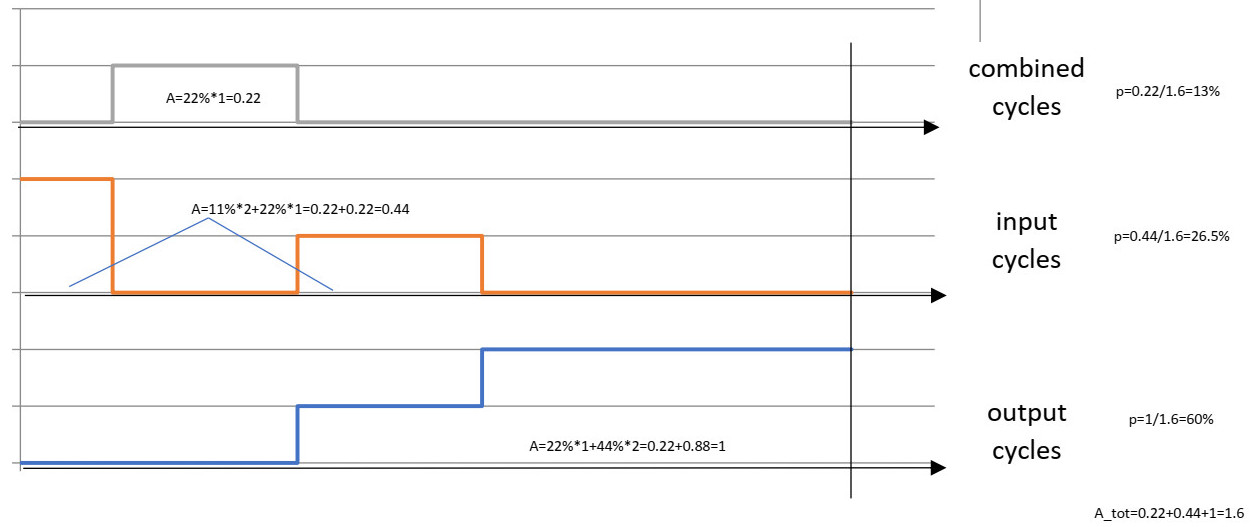
I diagrammet visas ett trädliknande diagram men gjort i sk

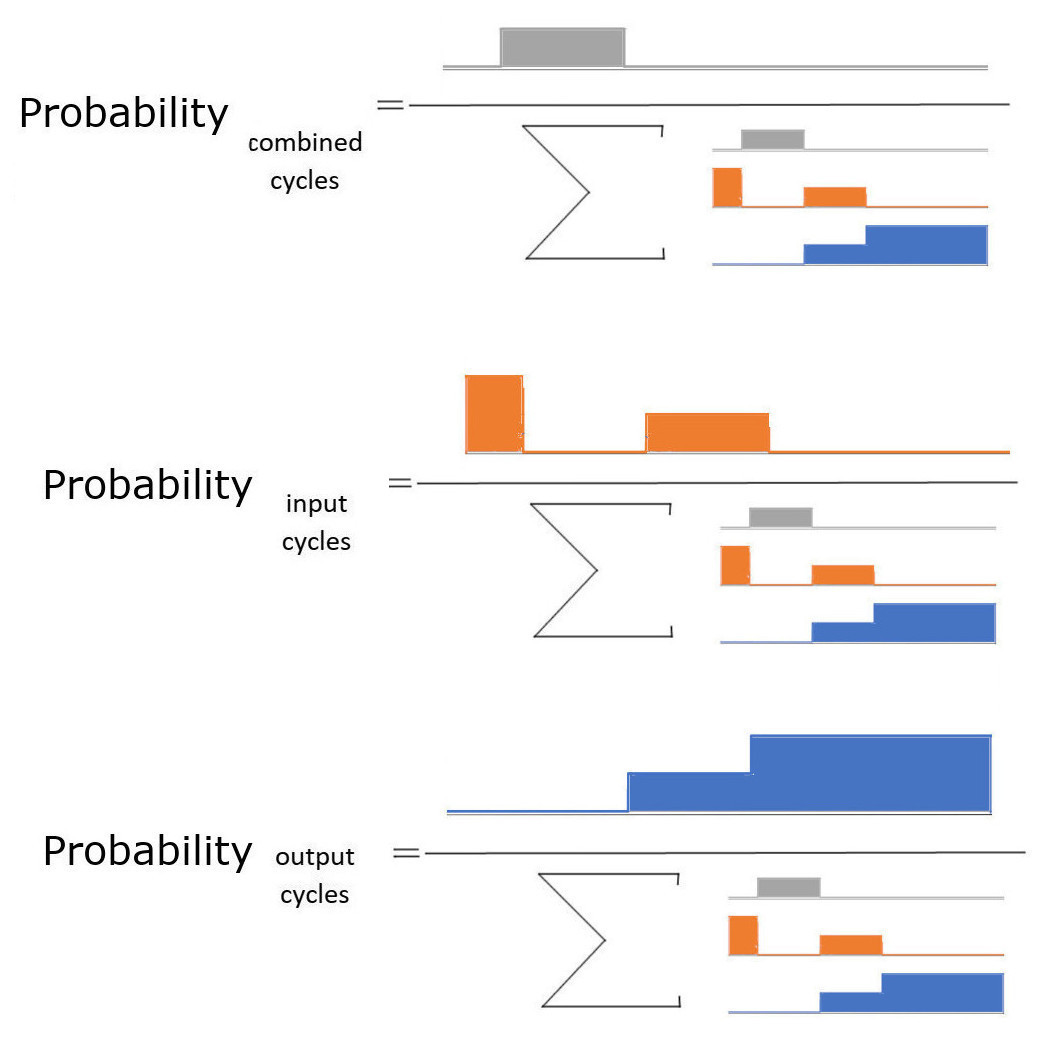
Sannolikheten för olika händelser (kombinerade, inmatning, utgång) är området för respektive händelse. Dividerat med området för alla händelser tillsammans.

Nästa steg i granskningen är att lägga till ett ytterligare steg, så att vi har 3 på varandra följande händelser. Den kombinerade cykeln visas nu tre gånger i det totala antalet åtta olika möjliga händelser. Så beroende på antalet på varandra följande händelser är möjligheterna alltid 2 upphöjt till antalet händelser. Följaktligen är kedjan av 3 på varandra följande inmatningshändelser 1/3 * 1/3 * 1/3 = 1/27 0,037 = 3,7%, vilket inte är ett stort nummer.

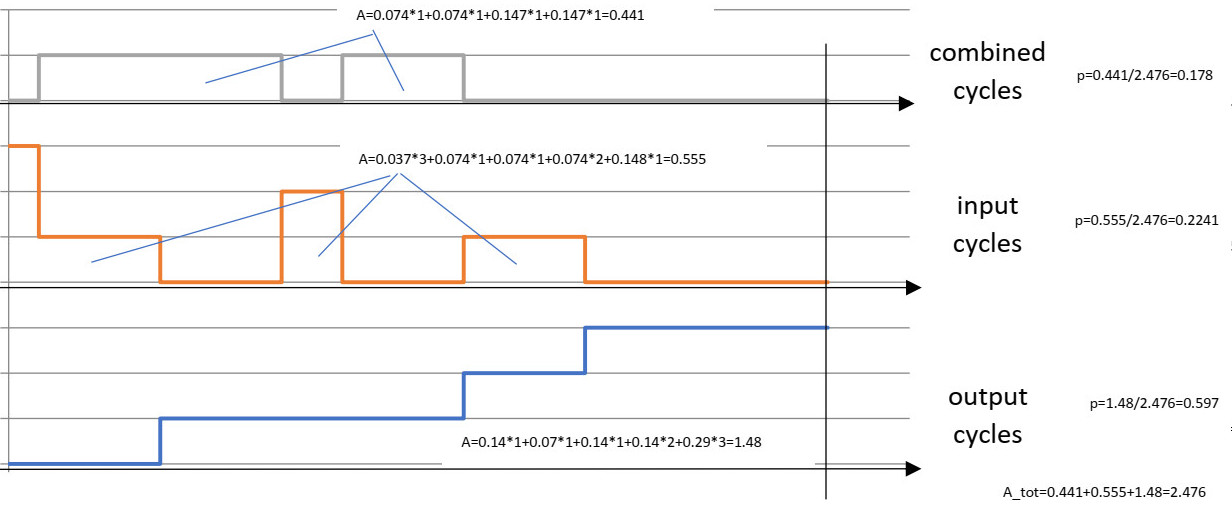
Så med 3 på varandra följande händelser är sannolikheten för den kombinerade cykeln 18%, sannolikheten för inmatningscykeln är 22% och sannolikheten för utgångscykeln är 60% och summan av alla sannolikheter är naturligtvis 100%. Vi kan också se att vår "trappstegskurva" har ett steg mer , totalt tre steg , men den kombinerade cykelkurvan har bara ett steg.

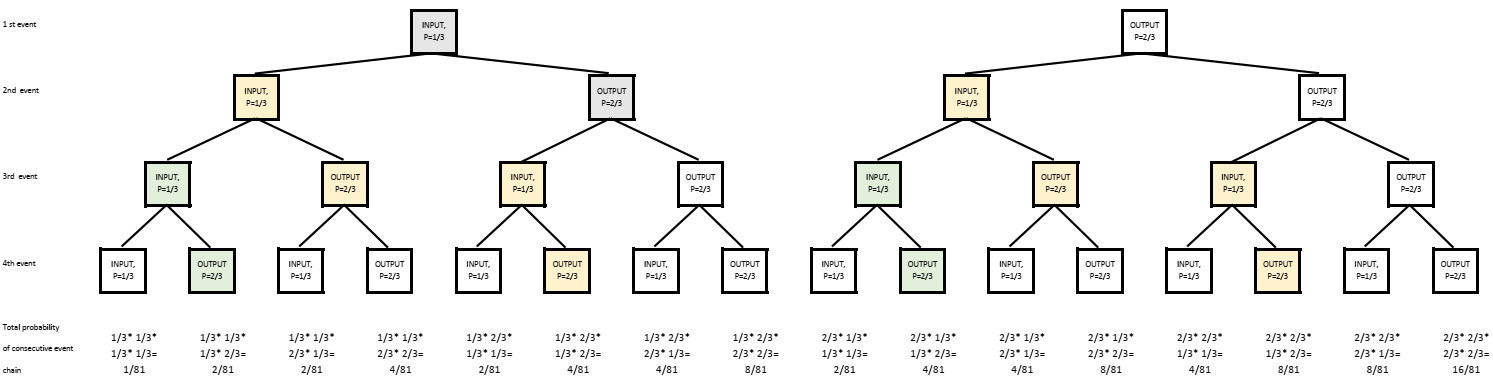
Eftersom vi nu har en rutin med denna procedur och vi blir mer och mer nyfikna kan vi fortsätta att göra det trädliknande diagrammet även med fyra på varandra följande steg.

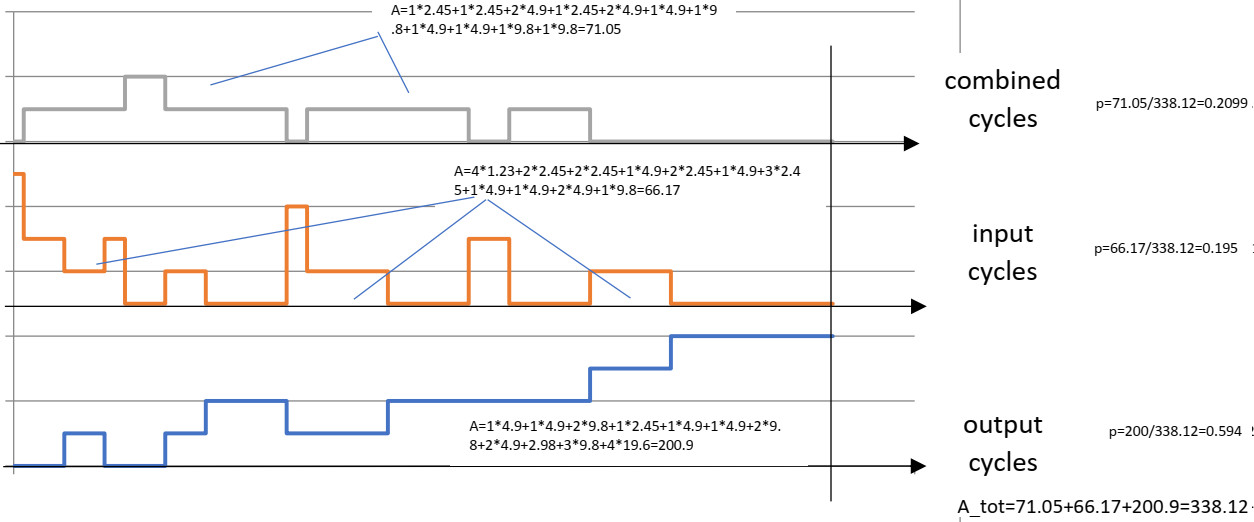
Tyvärr finns det ett problem med utrymmet i pappersbreddens riktning, det verkar omöjligt att rymma fler grenar i detta trädliknande diagram . Men sannolikhetsschemat kan fortsätta, även om stegbredden blir mindre och mindre. Det ger en kvantitativ översikt över hur många kombinerade cykler som kan uppnås jämfört med inmatnings- och utgångscykeln, eftersom områdena under de tre olika kurvorna jämförs.

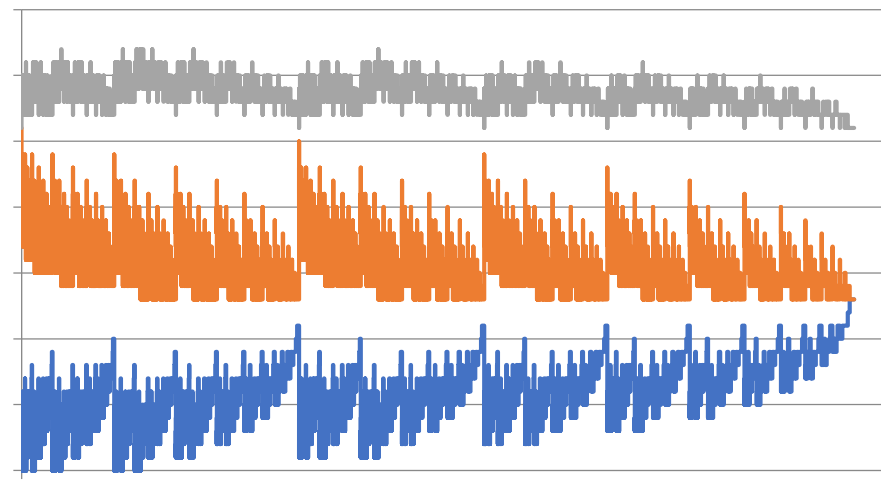
Genom att fortsätta öka antalet händelser närmar sig sannolikheten för den kombinerade cykeln 26%, sannolikheten för inmatningscykeln är 16% och sannolikheten för utgångscykeln når cirka 58%.

Hittills har alla tankar baserats på antagandet att fabriken körs 24 timmar om dygnet och produktionen under dagtid är 12 timmar per dag. En annan fråga är hur situationen skulle se ut när dagtiden är 16 timmar, vilket motsvarar en dag med tre skift där två skift kan användas för lastningsaktiviteter. Är det möjligt att, om lastningen utförs även 24 timmar om dygnet, alla cykler kan utföras i kombinerat läge?

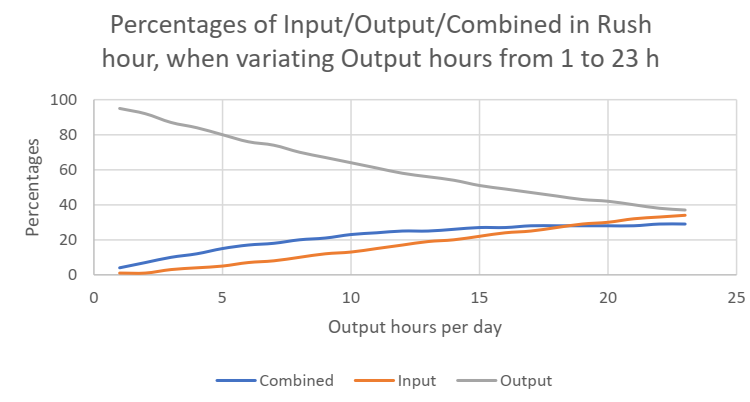
Denna kurva, där utgångstiden under dagtid är variabel, är något teoretisk eftersom den också visar en orealistisk situation som, till exempel när mycket få utgångstimmar per dag (säg bara 1 timme) innebär att under rusningstid måste nästan alla rörelser vara utgångsrörelser, så inga kombinationer är möjliga och inmatning är inte möjlig heller . Men är ett ganska orealistiskt scenario. I den andra änden av kurvan är proportionerna av de olika rörelserna (inmatning, utgång och kombinerade) ganska jämna, nästan som 1 /3 - 1/3 - 1 /3 .

Program Area import numpy class subprogram: def __init__(self, prob_p , prob_q , j, i): i=int(i) j=int(j) draw=numpy.ndarray(shape=(i,j), dtype=float) marker=numpy.ndarray(shape=(i,j), dtype=bool) combined_cycle=numpy.zeros(shape=(i), dtype=int) output_cycle=numpy.zeros(shape=(i), dtype=int) input_cycle=numpy.zeros(shape=(i), dtype=int) probability=numpy.ones(shape=(i), dtype=float) probability_integral=numpy.zeros(shape=(i+1), dtype=float) probability_integral_fin=numpy.zeros(shape=(i+1), dtype=float) # I want to fill an array with two dimensions with a variable, #which depends on the column and # and the row # column is i this represents all the possible different alternations of consecutive event paths # row is j this is how many consecutive events we are calculating. This is limited # by the computer capacity ( roundabout 13 consecutive event usually otherwise waiting time gets long) # in the start the program generates a pattern into a variable "draw" # draw in the meaning "draw a ticket" # draw[possible path of consecutive events][number of the step within the path of event] can be either input or output for row in range(j) : j_s=row+1 for column in range(i): print(' ',end='') u=2**j_s w=u/2 v=1+column%u if v>w: draw[column][row]=prob_q else: draw[column][row]=prob_p #print(draw[column][row], end='') #print("\n") for column in range(i): row=0 while row<(j-1): if (draw[column][row]==prob_q and draw[column][row+1]==prob_p): marker[column][row]= True marker[column][row+1]= True combined_cycle[column]+=1 row+=2 continue else: marker[column][row]= False marker[column][row+1]= False #import pdb; pdb.set_trace() row+=1 for column in range(i): for row in range(j): if (draw[column][row]==prob_q and marker[column][row]==False): input_cycle[column]+=1 elif(draw[column][row]==prob_p and marker[column][row]==False): output_cycle[column]+=1 #Probability of one chain of consecutive event for column in range(i): for row in range(j): if(draw[column][row]==prob_q): probability[column]*=prob_q else: probability[column]*=prob_p # to make an integral over all probability of one chain of consecutive event # which then in result must be 1 over all events for column in range(i): for counter in range(column): #import pdb; pdb.set_trace() probability_integral[column]+=probability[counter] for column in range(i): #import pdb; pdb.set_trace() probability_integral_fin[column-1]=probability_integral[column] probability_integral_fin[i-1]=1 #counter=0 #for column in range(i): # counter +=probability[column] * combined_output_input_cycle[column] #Area_combined_output_input_cycle = counter # 3 Times the Area for each combination # That is then resulting to the reach end result of all # Calculating the total area for each of COMBINE cycles #The Areas have no real meaning by themselfes! counter=0 for column in range(i): counter +=probability[column] * combined_cycle[column] Area_combined_cycle = counter # Calculating the total area for each of OUTPUT cycles counter=0 for column in range(i): counter +=probability[column] * output_cycle[column] Area_output_cycle = counter # Calculating the total area for each of INPUT cycles counter=0 for column in range(i): counter +=probability[column] * input_cycle[column] Area_input_cycle = counter # So the total area is the sum of all the areas : Total_Area=Area_combined_cycle+Area_output_cycle+Area_input_cycle # And the relative areas of each different cycle types are end result Relative_Area_combined_cycle=Area_combined_cycle/Total_Area Relative_Area_output_cycle=Area_output_cycle/Total_Area Relative_Area_input_cycle=Area_input_cycle/Total_Area # Printouts for debugging # afterwards maybe only the important values would be exported out of this function or module #for row in range(j): #for column in range(i): #print(' ',end='') #print(marker[column][row], end='') #print("\n") #print("\n") ''' for column in range(i): print(combined_cycle[column], end='') print(' ', end='') print("\n") for column in range(i): print(output_cycle[column], end='') print(' ', end='') print("\n") for column in range(i): print(input_cycle[column], end='') print(' ', end='') print("\n") for column in range(i): print(probability_integral_fin[column], end='') print(' ', end='') print("\n") ''' # #print(Relative_Area_combined_cycle) #print(Relative_Area_output_cycle) #print(Relative_Area_input_cycle) self.comb=Relative_Area_combined_cycle self.out=Relative_Area_output_cycle self.inp=Relative_Area_input_cycle # MAIN PROGRAM if __name__ == '__main__': print('The input is done 24h per day') hours_output=input('How many hours per day output is done ? ') hours_output=float(hours_output) probability_p=24/(24+hours_output) # probability for input probability_q=1-probability_p # probability for input a=13 # how many events are following each other b=2**a # the amount of different paths tulos=subprogram(probability_p , probability_q , a, b) print('\n') print('Probability for combined cycle ', end='') print(tulos.comb) print('Probability for output cycle ', end='') print(tulos.out) print('Probability for input cycle ', end='') print(tulos.inp)

För att beräkna de ovanstående diagrammen användes ett program med listning i Python-språket.