丹尼尔·卡尼曼(Daniel Kahneman)的《思考,快与慢》一书给我留下了深刻的印象。 主要观点是人类大多处于自动模式,他们的控制系统主要是本能的。卡尼曼称这个系统为“系统1”。 可以把它想象成你脑子里有一个小机器人,它只为最常见的任务编程。 比如系鞋带、刷牙等。但是 在人类这台奇妙的机器内部,还有另一个“机器人”,卡尼曼称之为“系统2”,它有一个更复杂的程序, 基于分析和基于分析的逻辑反应集。他最引人注目的例子是,如果有人问你, 2 x 2是多少,你不需要思考。但当有人问你,24 x 17是多少时,你没有答案。 你需要拿出一张纸,在纸上进行计算。
我强烈想起了用于电子控制数控机床的“级联控制”。在这些 控制中,有一个外部(反馈)环路和一个内部(反馈)环路,它们是嵌套的。 为了级联控制的正确运行,外环必须比内环慢。 这意味着内环的时间常数必须更小。 所以我本能地认为人类是级联控制的,外部控制是系统2,内部是系统1。
不知怎的,我偶然发现了这个例子。还有另一本书,《特拉赫滕伯格快速数学系统》, 它解释了如何在脑海中进行24 x 17这样的计算, 而不需要使用纸和笔。
用括号将两个外部数字和两个内部数字连接起来。
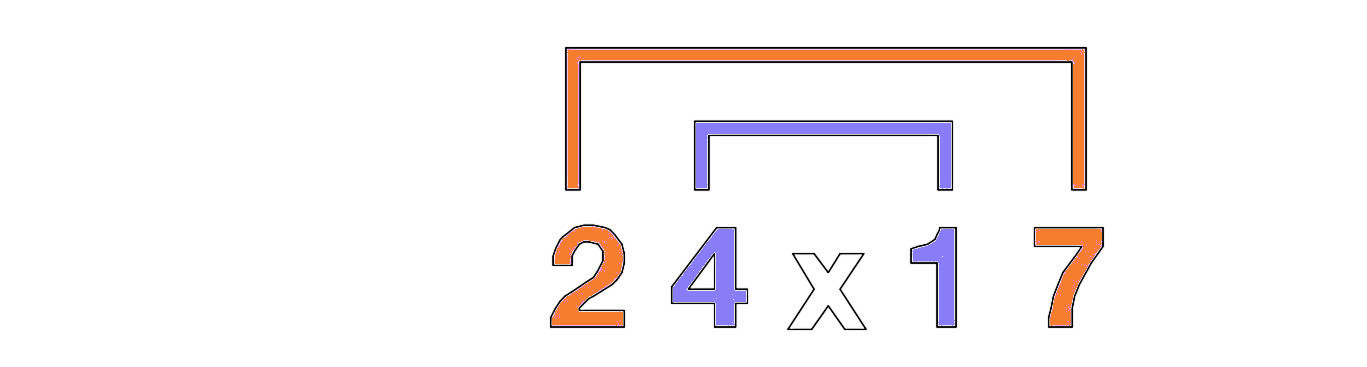
将两个外部数字相乘2 x 7 = 14,然后将两个内部数字相乘4 x 1 = 4,并将这两个数字相加,14 + 4 = 18。 最终结果将放入一个由4个占位符组成的方案中。18放在中间的两个占位符中。
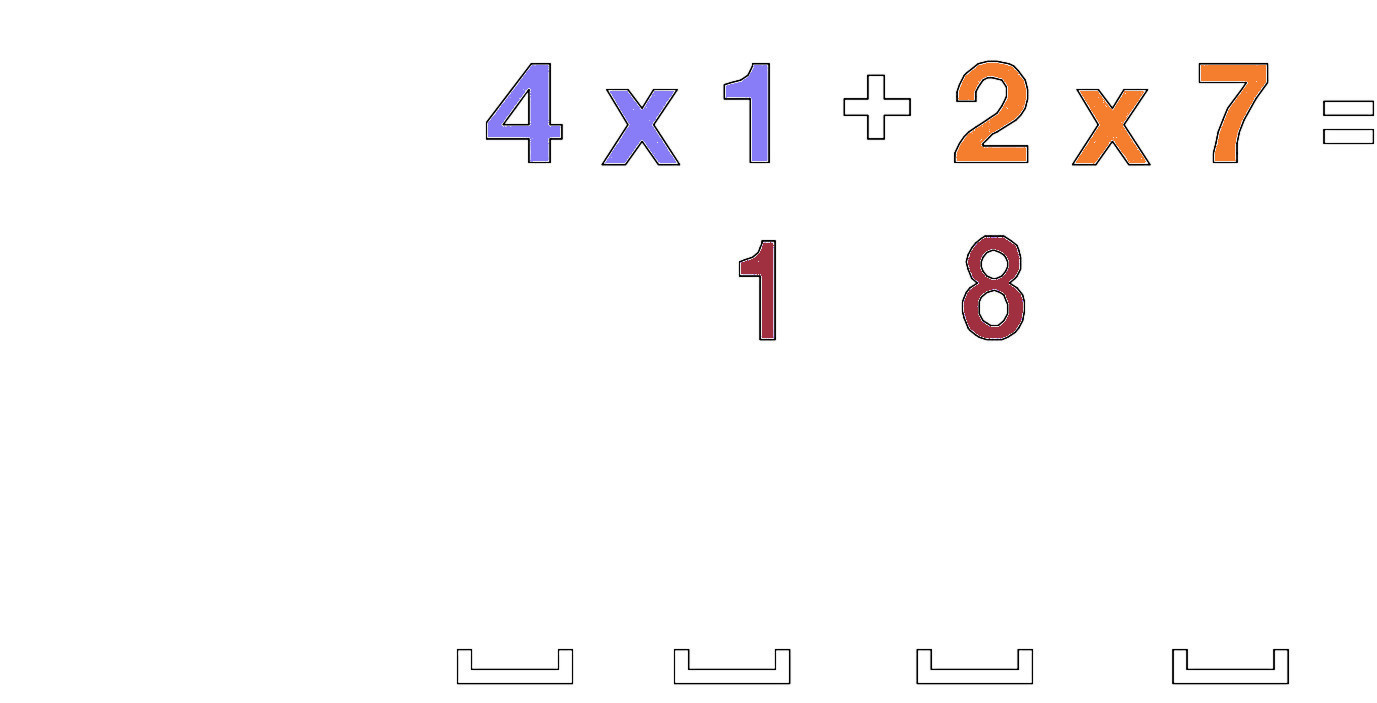
然后将每个数字的十位数相乘2 x 1 = 2,并将其放入左侧的两个占位符中。
然后将每个数字的最后一位相乘4 x 7 = 28,并将其放入右侧的两个占位符中。
现在,你需要将这三个乘法结果相加
我们将2 + 8 = 10相加,得到1,进位到下一列,并在该位置写下0。
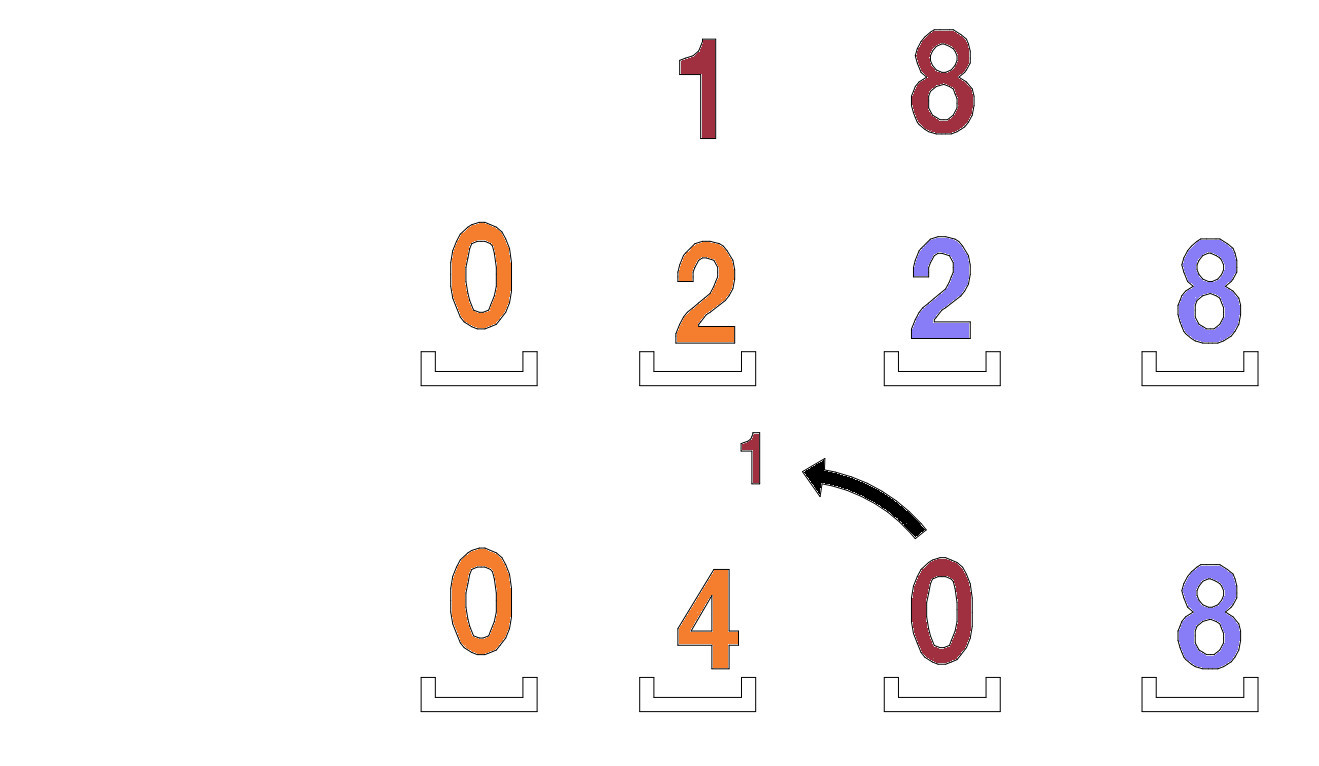
所以,最终结果是24 x 17 = 408。
对我来说,在脑海中进行这些计算仍然很困难,但当我把数字写在纸上时, 它比我在学校学到的系统更快。我尝试过在脑海中进行计算,但我 仍然觉得它很容易出错,尽管我不时会进行一些练习。最重要的是,我 往往会忘记进位。然而,在工作中,我仍然更喜欢使用我的惠普计算器和Excel, 因为它们只占用我大脑中的太多内存空间。我只是必须为所有绘图工作节省我的“系统2”, 这些工作必须与计算同时进行。
输入你自己的数字,然后按下按钮,看看计算是如何完成的。
*
| 1 | 8 | x | 2 | 4 | = | ||||||
| 将两个外部数字相乘,然后将两个内部数字相乘,并将这两个数字相加。 最终结果将放入一个由4个占位符组成的方案中。结果放在中间的两个占位符中。 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | x | 2 | + | 1 | x | 4 | = | ||||
| 2 | 0 | ||||||||||
| 然后将每个数字的十位数相乘,并将其放入左侧的两个占位符中。 | |||||||||||
| 1 | x | 2 | = | 2 | _ | _ | |||||
| 然后将每个数字的最后一位相乘,并将其放入右侧的两个占位符中。 | |||||||||||
| 8 | x | 4 | = | _ | _ | 3 | 2 | ||||
| 现在,你需要将这三个乘法结果相加 | |||||||||||
| 2 | 0 | ||||||||||
| 2 | 3 | 2 | |||||||||
| 最终结果是 | |||||||||||
| ------------------------------ | |||||||||||
| 4 | 3 | 2 | |||||||||
点击左右箭头,查看计算如何从开始到结束进行
以下段落摘自书中:Valtteri Suomalainen, Marianna Wallinheimo (toim.): Sauna Syyriassa, Recallmed 1995.
埃及的牧羊人,文盲且缺乏建议,在羊交易中值得一看。这是由于他们的乘法方法令人难以置信, 委婉地说。我在大马士革的时候听说过它,但我不理解,坦率地说,我现在仍然不理解。交易是这样进行的: 买卖双方坐在沙地上,面对面,用棍子在地上画一个十字架。在经历了阿拉伯文化特有的讨价还价仪式后, 他们最终就价格达成一致。假设每只60第纳尔买14只羔羊。在十字架上方并排放置与羊数量相等的小石头, 另一侧放置商定的第纳尔数量。现在开始从一侧加倍石头的数量,从另一侧减半(顺便说一句, 无论你从哪一侧开始减少和增加都无所谓)。例如,如果必须将数字7减半,当然会得到三点五, 但你根本不会计算半个(你不能把石头减半)。当减少的一侧不可避免地以数字1结束时, 接下来是最不可思议的操作:在要减少的一侧,找到所有符号数量为偶数的石堆。由于偶数是“不洁”, 这些石头连同对面的一侧一起被简单地移除。然后只需将加倍一侧的石头相加。结果总是正确的,简直像魔法一样。 即使是我的数学老师也无法解决这种方法,但他说当然有一个自然的解释。我尝试了所有可能的数字, 这种方法总是有效。我用几个例子演示了这种奇怪的计算方法。能做到的人就去发现吧。
我在以下网站上找到了这种方法