Daniel Kahnemans bok "Tänka, snabbt och långsamt" har gjort ett enormt intryck på mig. Huvudidén är att människor mestadels fungerar i automatiskt läge och deras styrsystem är mestadels instinktivt. Kahneman kallar detta system för "System 1". Det kan föreställas som en liten robot i ditt huvud, som bara är programmerad för de vanligaste uppgifterna. Som att knyta skosnören, borsta tänderna, etc. Men inne i den underbara mänskliga maskinen finns också en annan "robot", som Kahneman kallar "System 2" som har ett mer komplicerat program, baserat på analys och en logisk reaktion baserad på analys. Hans mest slående exempel är att om du blir tillfrågad, vad är 2 x 2, behöver du inte tänka på det ytterligare . Men när du blir tillfrågad, vad är 24 x 17, har du inget svar. Du skulle behöva ta fram ett papper och göra beräkningen på papperet.
Jag påminner starkt om "kaskadstyrning" som används till exempel i CNC-maskiner med elektronisk styrning. I dessa styrningar finns en yttre (feedback) loop och en inre (feedback) loop, och de är inbäddade i varandra. Den yttre feedback-loopen måste vara långsammare än den inre loopen för att kaskadstyrningen ska fungera korrekt. Detta innebär att den inre loopens tidskonstant måste vara mindre. Så jag tror instinktivt att människor styrs av kaskad, den yttre feedbacken är system 2 och den inre feedbacken är system 1.
På något sätt stötte jag på detta exempel. Det finns en annan bok, " Trachtenbergs snabba multiplikationssystem", som bara förklarar hur man gör beräkningar som 24 x 17 i ditt huvud, utan att använda papper och penna.
Skriv ner det med klamrar som förbinder de 2 yttre numren och de 2 inre numren.
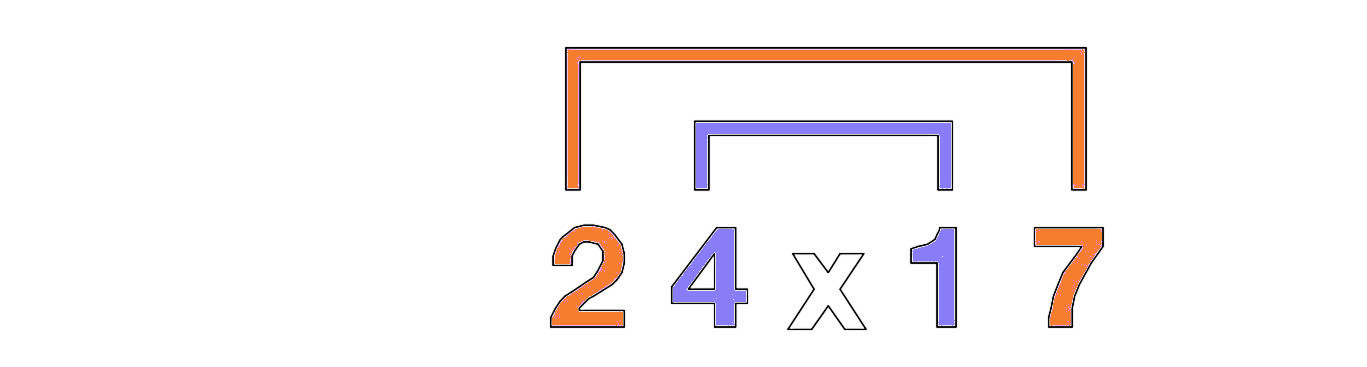
Multiplicera de 2 yttre numren 2 x 7 = 14 och sedan de 2 inre numren 4 x 1 = 4 och lägg till dessa 2 nummer, 14 + 4 = 18 Det slutliga resultatet kommer att placeras i ett schema med 4 platshållare. 18 placeras i de två mittersta platshållarna.
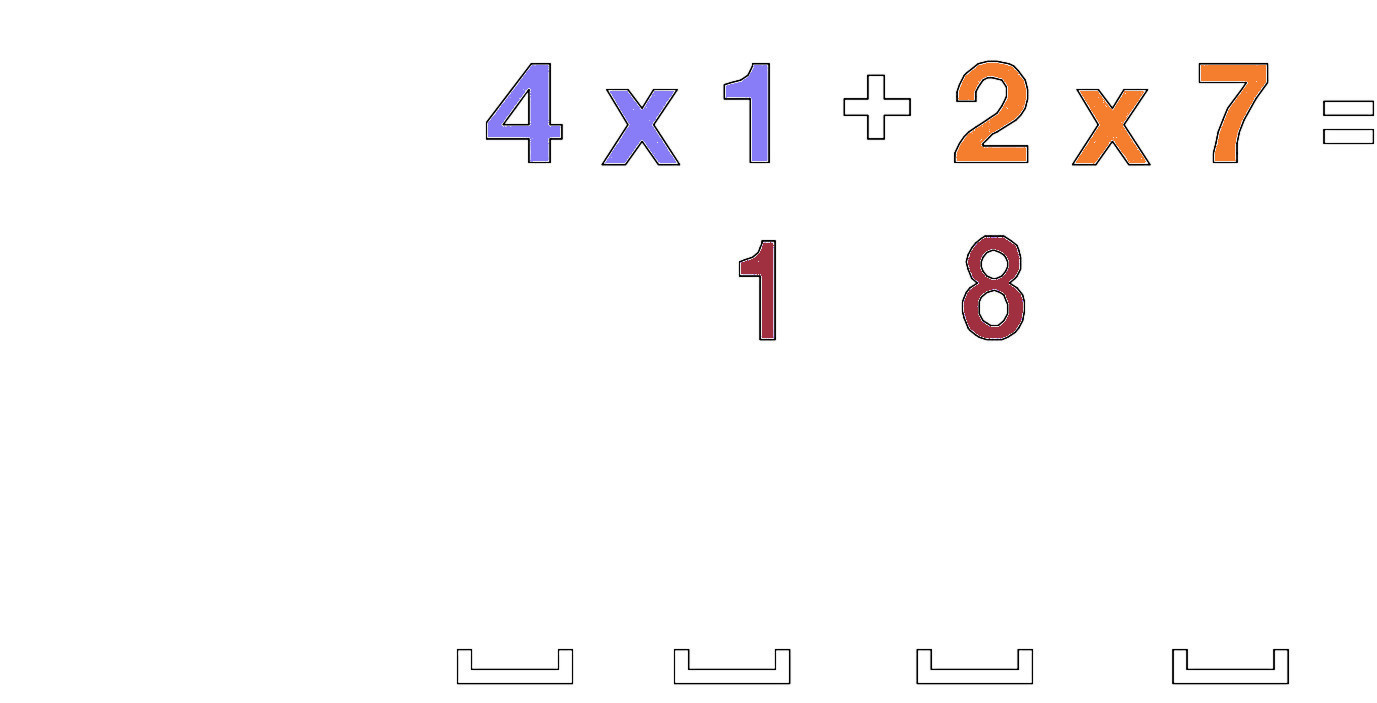
Multiplicera sedan tiotalsiffrorna för varje nummer 2 x 1 = 2 och placera det i de två vänstra platshållarna.
Multiplicera sedan de sista siffrorna för varje nummer 4 x 7 = 28 och placera dem i de två rätta platshållarna.
Nu måste du lägga till dessa tre multiplikationsresultat
Vi lägger ihop 2 + 8 = 10, vilket ger oss 1 som vi behöver bära över till nästa kolumn, och vi skriver 0 på platsen.
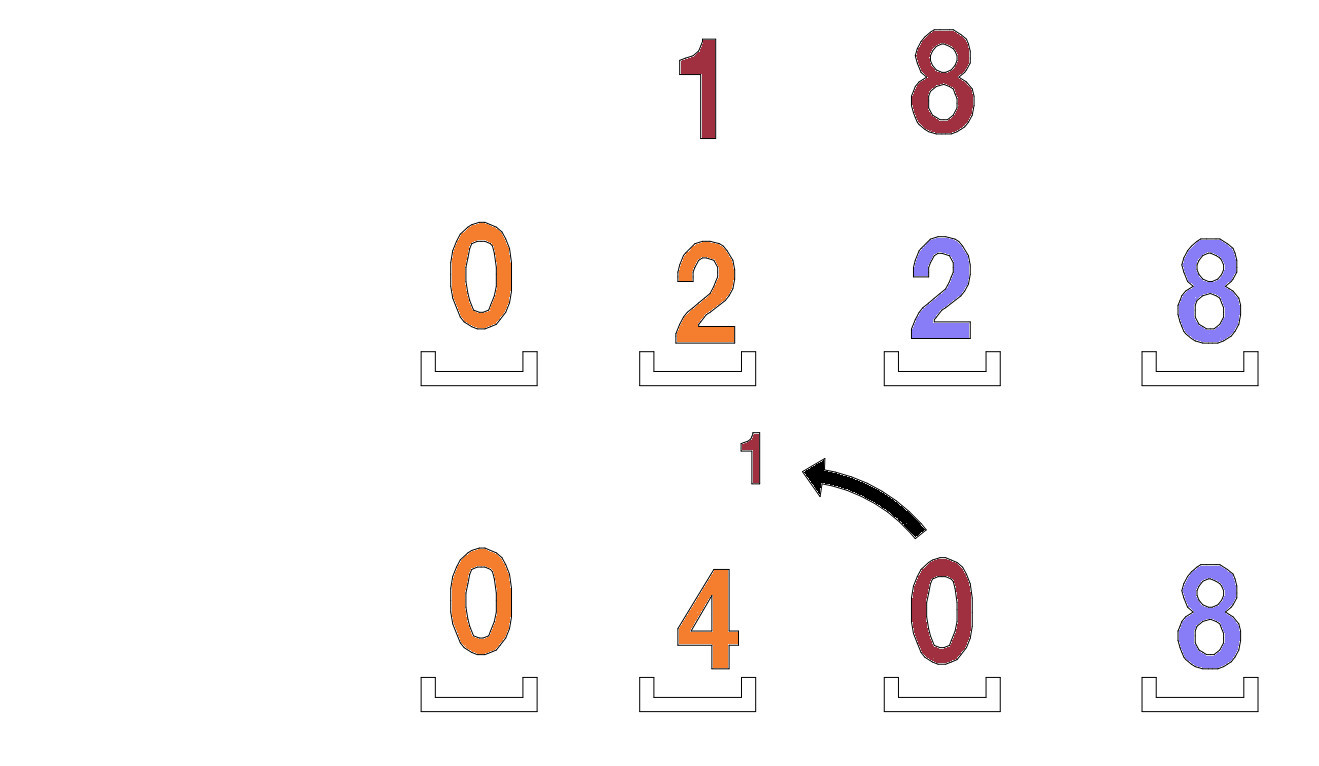
Så det slutliga resultatet är 24 x 17 = 408.
För mig är det fortfarande svårt att göra dessa beräkningar i huvudet men när jag skriver siffrorna på papper, är det snabbare än systemet jag lärde mig i skolan. Jag har försökt göra beräkningarna i mitt huvud men jag hittar det fortfarande ganska benäget för fel, även om jag då och då gör några repetitioner. Framför allt jag tenderar att glömma överföringen. Under mitt arbete föredrar jag dock fortfarande min HP-räknare och Excel, det tar bara för mycket minnesutrymme i mitt huvud. Jag måste bara spara mitt "System 2" för all ritning arbete, som måste utföras samtidigt med beräkningarna.
Ange dina egna siffror och tryck på knappen för att se hur beräkningen utförs.
*
| 1 | 8 | x | 2 | 4 | = | ||||||
| Multiplicera de 2 yttre numren och sedan de 2 inre numren och lägg till dessa 2 nummer. Det slutliga resultatet kommer att placeras i ett schema med 4 platshållare. Resultatet placeras i de två mittersta platshållarna. | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | x | 2 | + | 1 | x | 4 | = | ||||
| 2 | 0 | ||||||||||
| Multiplicera sedan tiotalsiffrorna för varje nummer och placera det i de två vänstra platshållarna. | |||||||||||
| 1 | x | 2 | = | 2 | _ | _ | |||||
| Multiplicera sedan de sista siffrorna för varje nummer och placera dem i de två rätta platshållarna. | |||||||||||
| 8 | x | 4 | = | _ | _ | 3 | 2 | ||||
| Nu måste du lägga till dessa tre multiplikationsresultat | |||||||||||
| 2 | 0 | ||||||||||
| 2 | 3 | 2 | |||||||||
| det slutliga resultatet är | |||||||||||
| ------------------------------ | |||||||||||
| 4 | 3 | 2 | |||||||||
klicka på höger- och vänsterpilarna för att se hur beräkningen går från början till slut
Följande stycke är hämtat från boken :Valtteri Suomalainen, Marianna Wallinheimo (toim.): Sauna Syyriassa, Recallmed 1995.
Egyptiska herdar, analfabeter och dåligt rådgivna, är ett skådespel att se i fårhandel. Detta beror på deras otroliga multiplikationsmetod, för att uttrycka det milt. Jag hörde talas om det när jag var i Damask us, men jag förstod det inte, och ärligt talat förstår jag det fortfarande inte. Så här går handeln till: köparen och säljaren sätter sig på sanden mittemot varandra och ritar ett kors på marken med en pinne. Efter att ha genomgått den prutningsceremoni som är karakteristisk för arabisk kultur, kommer de slutligen överens om priset. Säg 14 lamm för 60 dinarer styck. Ett antal små stenar lika med antalet får placeras sida vid sida ovanför korset, och det överenskomna antalet dinarer placeras på andra sidan. Börja nu dubbla antalet stenar på ena sidan och halvera på andra sidan (förresten, det är en fråga om vilken sida du börjar minska och öka från). Om till exempel siffran 7 måste halveras f år du naturl igtvis tre och en halv men du kommer helt enkelt inte att räkna halvor (du kan inte halvera stenar). När den minskande sidan oundvikligen slutar med siffran ett följer den mest otroliga manövern: på den minskande sidan, hitta alla stenhögar med ett jämnt antal symboler. Eftersom ett jämnt tal är "orent" tas dessa stenar helt enkelt bort, inklusive den motsatta sidan. Lägg sedan bara ihop stenarna på den dubbla sidan. Resultatet visar sig alltid vara korrekt, som genom magi. Även min mattelärare kunde inte lösa metoden men sa att det naturligtvis finns en naturlig förklaring. Jag har provat metoden med alla möjliga siffror och den fungerar alltid. Jag har demonstrerat denna märkliga beräkningsmetod med några exempel. Låt den som kan göra det ta reda på det.
Jag hittade detta sätt på följande webbplats