Kelly criterion simulator
In an experiment a group of persons were asked to participate at a lottery, in which the participiants can win and then double the wage in 60% of the cases, but in 40% of the case they lose the wagered part of their capital. For a start each participant was given 20 Dollars and then he had 30 minutes time to play the game. Theoretically, in this 30 minutes one could bet 300 times.

The result of this experiment? At the end, a third of the participants had less then at the start of the experiment, even more, 28 percent of the participants had lost all the capital and went bancrupt. Only 21 percent of the participants achieved the required required maximum of 250 Dollars, which should have been achieved at correct application of the Kelly criterium. Accordingly, the average payout of 91 Dollars was significantly below the expected value of 250 Dollars. 18 persons of the 61 participants of the experiment even put all their eggs in one basket, whereby the probability of a total loss went up to 40 percent. Whereas, when using the Kelly formula, the probability of a total loss is almost zero percent.
What would have been the optimum strategy, when using the Kelly criteria? What if, as in the described experiment, the probability of winning would be 60%, and the win-loss ratio would be 1 (Meaning, in case of winning the bet, the stake is doubled)? In this example, the percentage of the capital, which should be risked (wagered) should be 20 percent of the presently available money.
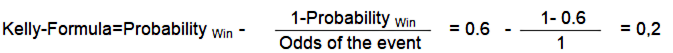
If you risk, as in this example, more then 20% of you money for a lottery, in the long run there is a risk to loose all your capital - even if the statistical chances are in your favor. On the other hand the average gain of a participant would be 4% per game round.
Here comes the simulator:
start from scratch