Pourquoi il n'est pas rentable de risquer tout son argent?

Critère de Kelly simulation

Dans une expérience, des personnes ont été invitées à participer à une loterie, dans laquelle les participants peuvent gagner puis doubler le salaire dans 60 % des cas, mais dans 40 % des cas, ils perdent la mise. Chaque participant recevait 20 dollars et disposait de 30 minutes pour jouer au jeu. Théoriquement, dans ces 30 minutes, on pourrait parier 300 fois.

Le résultat de cette expérience ? À la fin, un tiers des participants avaient moins qu'au début de l'expérience, voire plus, 28 % des participants avaient perdu tout le capital et avaient fait faillite. Seuls 21% des participants ont atteint le maximum requis de 250 dollars, qui aurait dû être atteint lors de l'application correcte du critère de Kelly. En conséquence, le paiement moyen de 91 dollars était nettement inférieur à la valeur attendue de 250 dollars. 18 personnes sur les 61 participants à l'expérience ont même mis tous leurs œufs dans le même panier, la probabilité d'une perte totale atteignant 40 %. Alors que, lors de l'utilisation de la formule de Kelly, la probabilité d'une perte totale est de presque zéro pour cent.

Quelle aurait été la stratégie optimale, en utilisant les critères de Kelly ? Que se passe-t-il si, comme dans l'expérience décrite, la probabilité de gagner serait de 60 % et le ratio victoire-perte serait de 1 (ce qui signifie qu'en cas de gain du pari, la mise est doublée) ? Dans cet exemple, le pourcentage du capital qui doit être risqué (misé) doit être de 20 % de l'argent actuellement disponible.

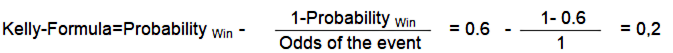
Si vous risquez, comme dans cet exemple, plus de 20% de votre argent pour une loterie, à long terme, il y a un risque de perdre tout votre capital - même si les chances statistiques sont en votre faveur. D'autre part le gain moyen d'un participant serait de 4% par tour de jeu.

Voici donc le programme de simulation: