Daniel Kahnemanin kirja "Ajattelu, nopeasti ja hitaasti", on tehnyt minulle valtavan vaikutuksen. Pääideana on, että ihmiset elelevät enimmäkseen automaattitilassa ja heidän ohjausjärjestelmä perustuu enimmäkseen vaistoihin. Kahneman kutsuu tätä järjestelmää "Systemi 1". Se voidaan kuvitella kuten pieni robotti pään sisällä, joka on ohjelmoitu vain kaikesta yleisimpiin tehtäviin. Kuten kengännauhojen sitominen, hampaiden harjaus jne. Mutta ihmisen ihmeellisen koneiston sisällä on myös toinen "robotti", jota Kahneman kutsuu "Systemi 2", jolla on monimutkaisempi ohjelma, joka perustuu analyysiin ja loogiseen reaktioon analyysin perusteella. Hänen silmiinpistävin esimerkki on, että jos sinulta kysytään, mikä on 2 x 2, sinun ei tarvitse miettiä sitä sen enempää. Mutta kun sinulta kysytään, mikä on 24 x 17, sinulla ei ole vastausta. Sinun olisi otettava paperi ja tehtävä laskelma paperille.
Minulle tulee mieleen ohjaustekniikassa käytetty "Kaskadiohjaus" joka käytetään esimerkiksi CNC koneiden ohjaukseen. Näissä ohjausjärjestelmissä on kytketty useampia ohjauspiiriä sarjaan ja sisäkkäin. Sisäinen ohjauselementti on nopeampi kuin ulommainen ohjauselementti. Tämä tarkoittaa, että sisäisen ohjauselementin aikavakion on oltava pienempiä, jotta kaskadiohjaus toimii. Niin että ajattelin, että ihminen on kaskadiohjattu järjestelmä, jossa uloin ohjainjärjestelmä on Systeemi 2 ja sisäinen ohjain on systemi 1.
Jotenkin tämä esimerkki aiheutti minulle päävaivaa . On nimittäin toinenkin kirja, "Trachtenbergin nopean kertolaskeman perusteet ", joka selittää vain kuinka tehdä 24 x 17 tapaiset laskelmat, ilman paperi ja lyijykynä, ihan vaan päässä.
Kirjoita numerot ylös ja yhdistää ne kaks ulkoiset numerot ja 2 sisäiset numerot sulkumerkeillä.
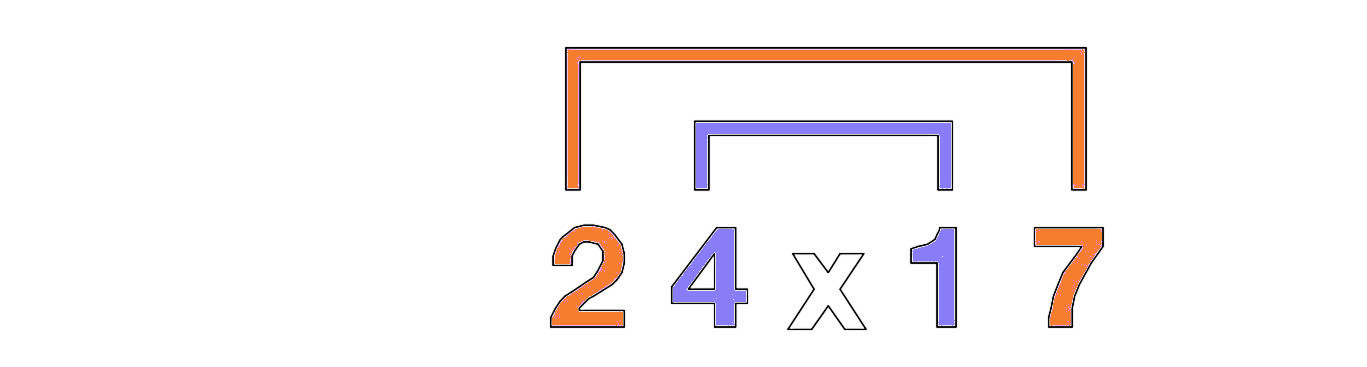
Kerro 2 ulompaa numeroa 2 x 7 = 14 ja sitten sisäiset 2 numeroa 4 x 1 = 4 ja ynnää nämä 2 numeroa, 14 + 4 = 18 Lopputulos asetetaan 4 paikkamerkkijärjestelmään, niin että 18 sijoitetaan kahden sisimmäisen paikkamerkin päällä.
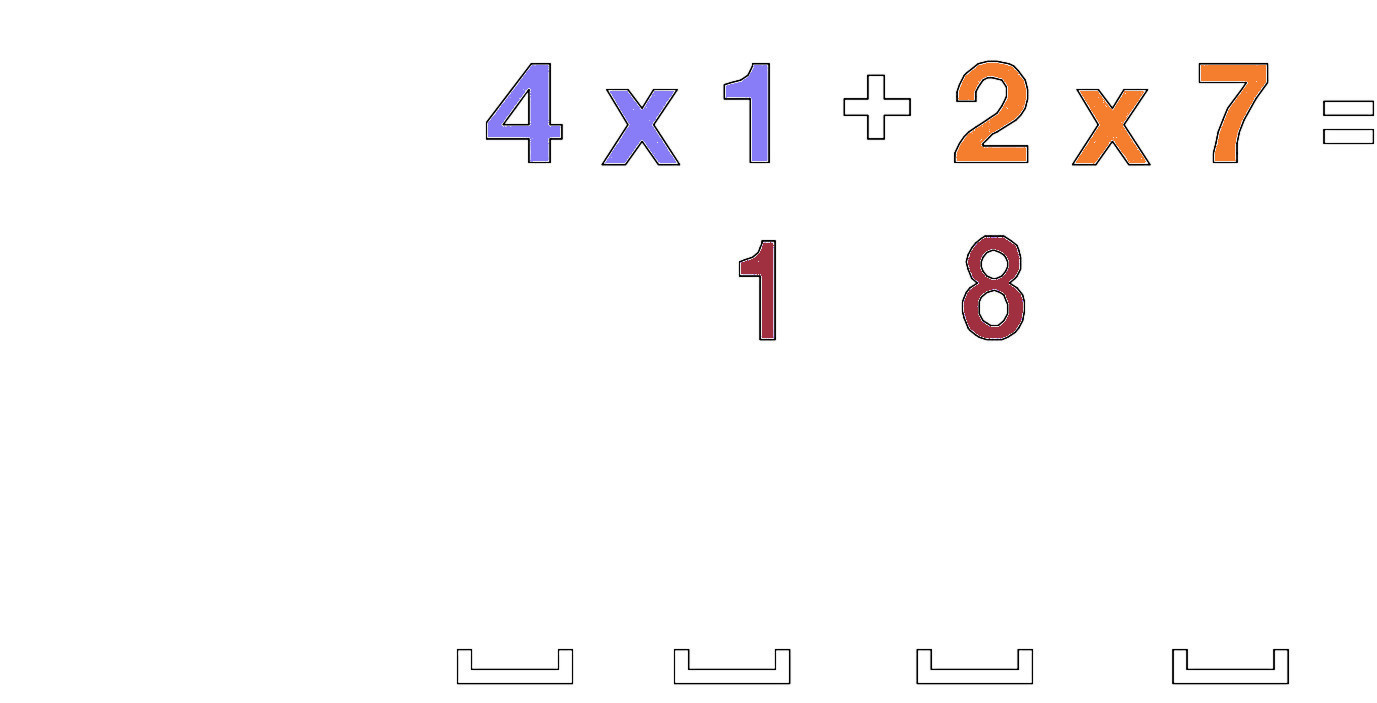
Kerro sitten jokaisesta luvusta kymmenes 2 x 1 = 2 ja laita se vasempaan kahteen paikkaan.
Sitten kerro kunkin numeron viimeiset numerot 4 x 7 = 28 ja laita se oikeisiin kahteen paikkaan.
Nyt sinun täytyy ynnätä näitten kolme kertolaskelman tulokset
Meidän täytyy ynnää 2 + 8 = 10, kirjoitetaan 0 ja siirretään 1 seuraavaan saraan.
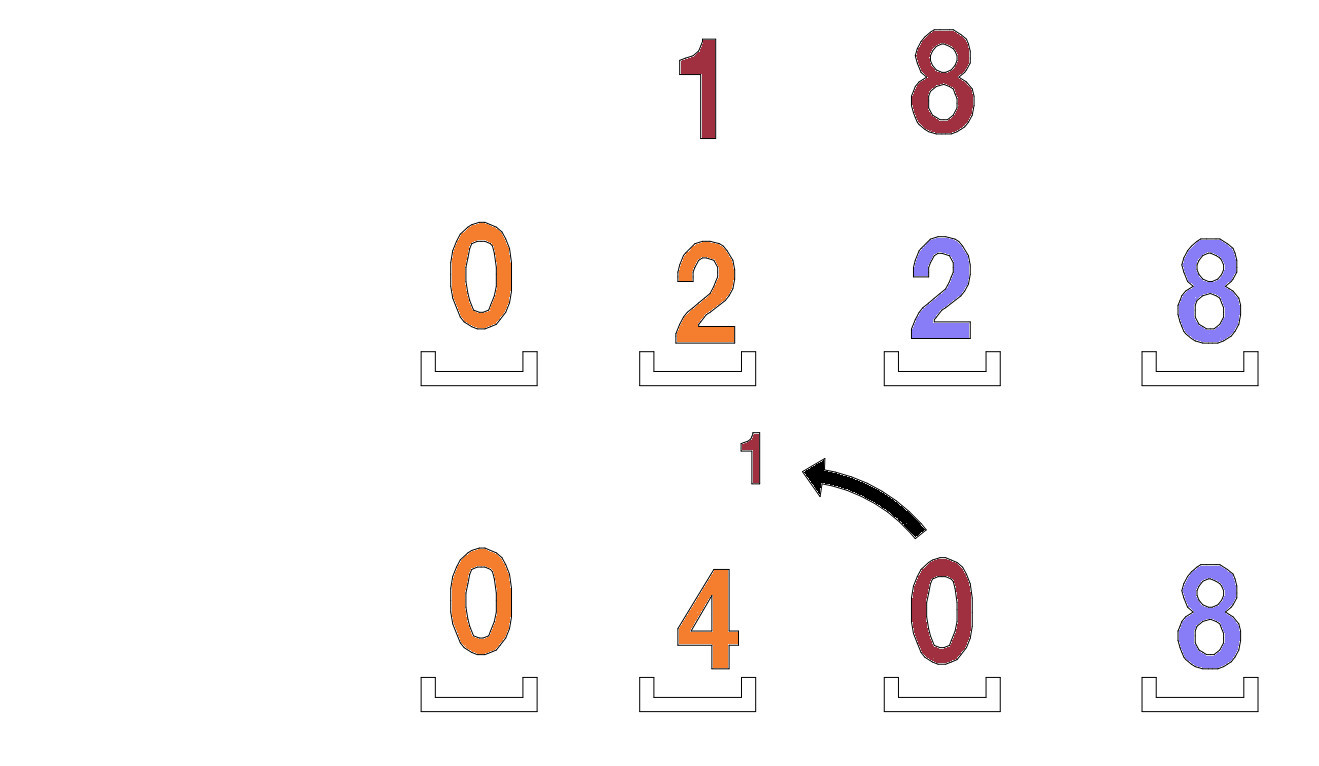
Joten lopputulos on 24 x 17 = 408.
Minulle on edelleen vaikea tehdä näitä laskelmia päässäsi, mutta kirjoittaessani numeroita paperille, se on nopeampi kuin järjestelmä, jonka oppin koulussa. Olen yrittänyt tehdä laskelmat päässäni, mutta minä pitää sitä edelleen melko alttiina virheille, vaikka ajoittain harjoitankin. Ennen kaikkea minä unohtaa kantaa. Työn aikana pidän silti parempana HP-laskinta ja Exceliä, se on vie vain paljon päätäni muistitilaa. Minun täytyy vain säästää "Järjestelmäni 2" kaikille piirustuksille työ, joka on tehtävä samanaikaisesti laskelmien kanssa.
Laita omat numerot ja katso miten tämä menetelmä toimii
*
| 1 | 8 | x | 2 | 4 | = | ||||||
| Kerro 2 sisäiset numerot ja sitten ulkoiset 2 numerot ja ynnää nämä 2 tulokset. Lopputulos asetetaan 4 paikkamerkkijärjestelmään, niin että sijoitetaan kahden sisimmäisen paikkamerkin päällä. | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 | x | 2 | + | 1 | x | 4 | = | ||||
| 2 | 0 | ||||||||||
| Kerro sitten jokaisesta luvusta kymmenekset ja laita se vasempaan kahteen paikkaan. | |||||||||||
| 1 | x | 2 | = | 2 | _ | _ | |||||
| Sitten kerro kunkin numeron viimeiset numerot ja laita se oikeisiin kahteen paikkaan. | |||||||||||
| 8 | x | 4 | = | _ | _ | 3 | 2 | ||||
| Nyt enää vaan ynnättävää ylläolevien kolmen kertolaskelmien tulokset | |||||||||||
| 2 | 0 | ||||||||||
| 2 | 3 | 2 | |||||||||
| Lopputulos on | |||||||||||
| ------------------------------ | |||||||||||
| 4 | 3 | 2 | |||||||||