Trachtenberg way of multiplikation

Daniel Kahneman's book Thinking, fast and slow", has made an huge impression to me. The main idea is, that humans are mostly running in automatic mode, and their control system is mostly instinctive. Kahneman calls this system the "System 1" It can be imagined like a small robot inside your head, which programmed for only the most common tasks. Such as tying your shoestrings, brushing your teeth, etc. But inside of the human wonderful machinery also exists another "robot", which Kahneman calls "System 2" which has a more complicated program, based on analysis and a logical reaction set based on the analysis. His most striking example is, that if you are asked, what is 2 x 2 , you don't have to think about it. But when you are asked, what is 24 x 17, you don't have any answer. You would have to take a paper and make the calculation on the paper.

I am strongly reminded of the "cascade control", used for instance at electronically controlled CNC machineries. In those controls there is an outer (feedback-) loop and an inner (feedback) loop and they are nested. The exterior loop must be slower then the interior loop for a correct functioning of the control. So I think instinctively, that humans are Cascade controled, the outer control is system 2 and the inner is system 1.

Somehow I stumbled over this example. There is another Book , "Trachtenberg speed system of basic mathematics", which just explains, how to do calculations of 24 x 17 in your head, without having to use paper and pencil.

Write it down with bracked connecting the 2 outer numbers and the 2 inner numbers.

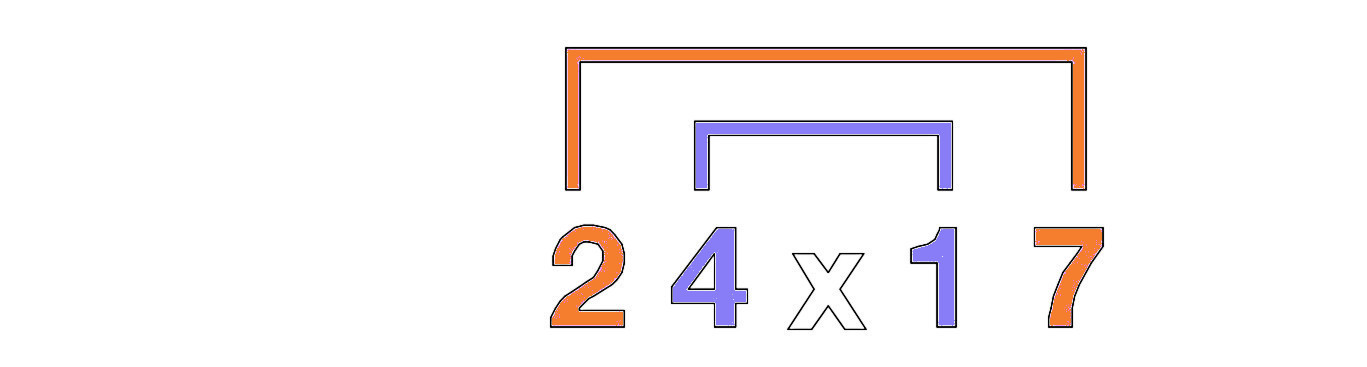
Multiply the 2 outer numbers 2 x 7=14 and then the inner 2 numbers 4 x 1 = 4 and add those 2 numbers, 14+4 =18 The end result will be put into a scheme of 4 placeholders. The 18 is put into the middle two placeholders.

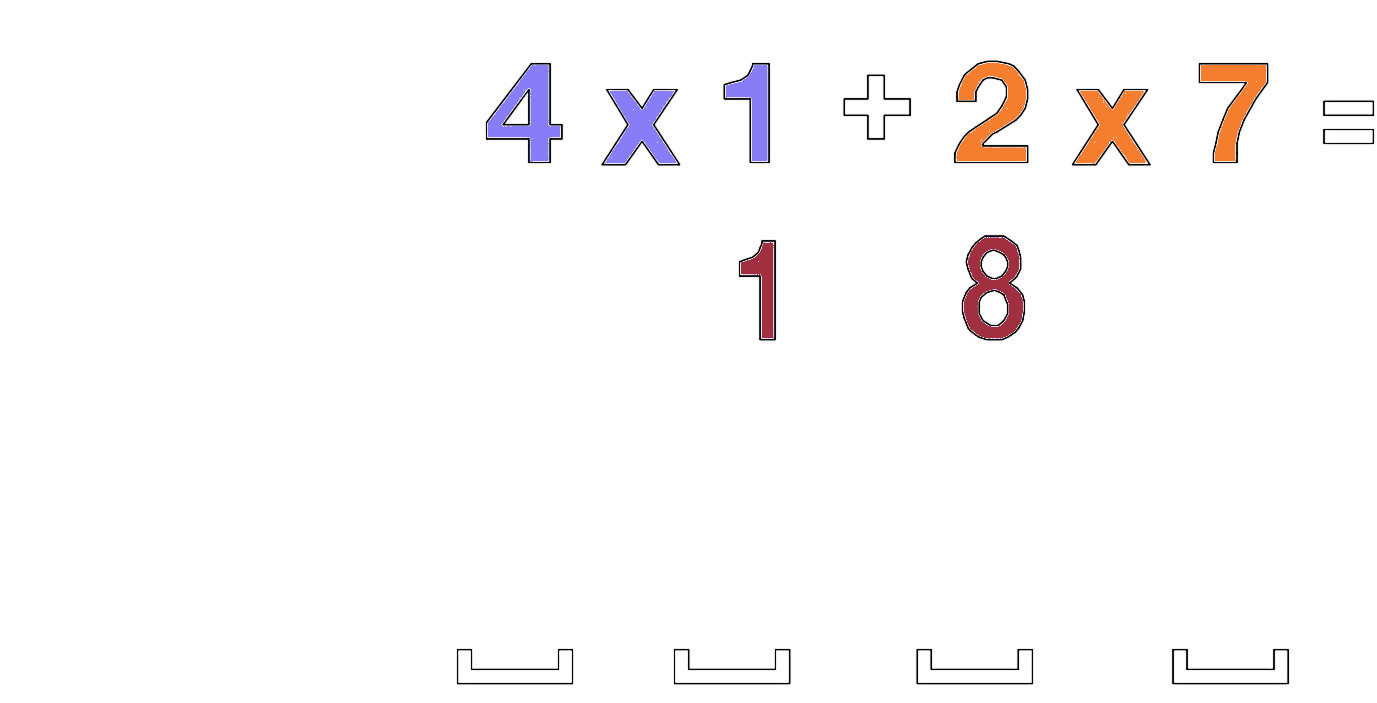
Then multiply the tens of each number 2 x 1 = 2 and put it into the left two placeholders.

Afterwards multiply the last digits of each number 4 x 7 =28 and put it into the right two placeholders.

Now, you have to add up the three multiplication results

We are adding the 2 + 8 = 10, that gives us 1 which carried on to the hundreds, and we write 0 to the place.

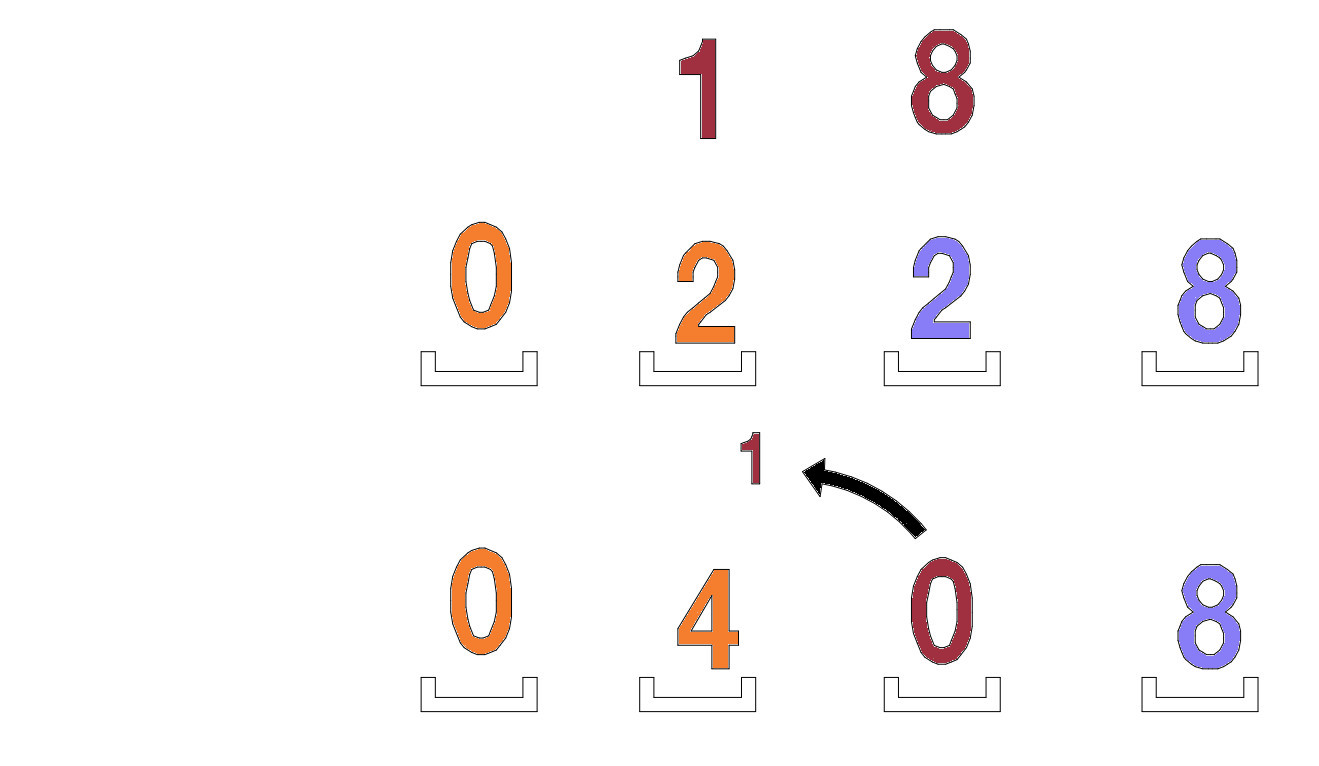
So, the end result is 24 x 17 = 408.

For me it is still hard to do these calculations in your head, but when writing down the numbers on paper, it is quicker then the system I learned at school. I have tried to do the calculations in my head, but I still find it quite prone to mistakes, although from time to time I do some rehearsals. Most of all, I tend to forget the carry. During my work, nevertheless, I still prefer my HP calculator and Excel, it's just takes too much of memory space in my head. I just have to economize my "System 2" for all the drawing work, which have to be done simultaneously to the calculations.

Put in your own numbers and press the button to see how the calculation is done.

*

Another way to multiply, so called Russian peasant method

click the right and left arrows to see how the calculation is progressing from start to end

The following paragraph is taken from the book : Valtteri Suomalainen, Marianna Wallinheimo (toim.): Sauna Syyriassa, Recallmed 1995.

Shepherds in Egypt, who are illiterate and ill-advised, are worthwhile watching when they are trading sheep. This is due to their, to put it mildly, incredible method of multiplication. I heard about it in my time in Damascus, but I did not understand it, and frankly I still don't. Here's what happens in a trade: buyer and seller sit down on the sand opposite each other and draw a cross on the ground with a stick. After going through the haggling ceremony of Arab culture, they finally come to an agreement on the price. Let's say 14 lambs for 60 dinars each. A number of small stones equal to the number of sheep are placed side by side above the cross, and the agreed number of dinars on the other side. Now they start by doubling the number of stones on one side and halving on the other (it doesn't matter of which side you start to reduce and increase, by the way.) If you have to halve the number 7, for example, you get three and a half, of course, but you simply don't count the halves (you can't halve the stones). When the decreasing side inevitably ends up with the number one, the most incredible manoeuvre follows: on the side to be reduced, all the piles of stones with an even number of symbols are sorted out. Since an even number is "unholy", these stones are simply removed, including the opposite side. Then just add up the stones on the doubled side. Quite magically, the result is always correct. Even my maths teacher could not solve the method, but said there was of course a natural explanation. I have tried the method with every possible number and it always works. I have demonstrated the strange calculation method with a few examples. Let anyone who can do it find out.

I found this way on the following website