Méthode de multiplication de Trachtenberg

Le livre de Daniel Kahneman "Système 1 / Système 2 : Les deux vitesses de la pensée", m'a fait une énorme impression. L'idée principale est que les humains fonctionnent principalement en mode automatique et leur système de contrôle est principalement instinctif. Kahneman appelle ce système le "Système 1" On peut l'imaginer comme un petit robot à l'intérieur de votre tête, qui ne programme que pour les tâches les plus courantes. Comme attacher vos cordons, vous brosser les dents, etc. Mais à l'intérieur de la merveilleuse machine humaine existe également un autre "robot", que Kahneman appelle "Systeme 2" qui a un programme plus compliqué, basé sur l'analyse et une réaction logique ensemble basé sur l'analyse. Son exemple le plus frappant est que si on vous le demande, ce qui est 2 x 2, vous n'avez pas à y penser. Mais quand on vous demande, qu'est-ce 24 x 17, vous n'avez pas de réponse. Il faudrait prendre un papier et faire le calcul sur le papier.

Je me rappelle fortement le "circuit de contrôle en cascade", utilisé par exemple dans les machines CNC à commande électronique. Les contrôles sont imbriqués, il existe une boucle externe (rétroaction) et une boucle interne (rétroaction). La boucle extérieure doit être plus lente que la boucle intérieure pour un bon fonctionnement de la contrôle en cascade. Cela signifie que la constante de temps de la boucle intérieure doit être plus petite. Je pense donc instinctivement que les humains sont le contrôle en cascade, le contrôle extérieur est le système 2 et l'intérieur est le système 1.

D'une certaine manière, je J'étais très inspiré pour cet exemple, parce que Il y a un autre livre, " Trachtenberg système de multiplication de vitesse", qui explique simplement, comment faire des calculs similaire de 24 x 17 dans votre tête, sans utiliser du papier et crayon.

Notez-le avec des crochets reliant les 2 numéros extérieurs et les 2 numéros intérieurs.

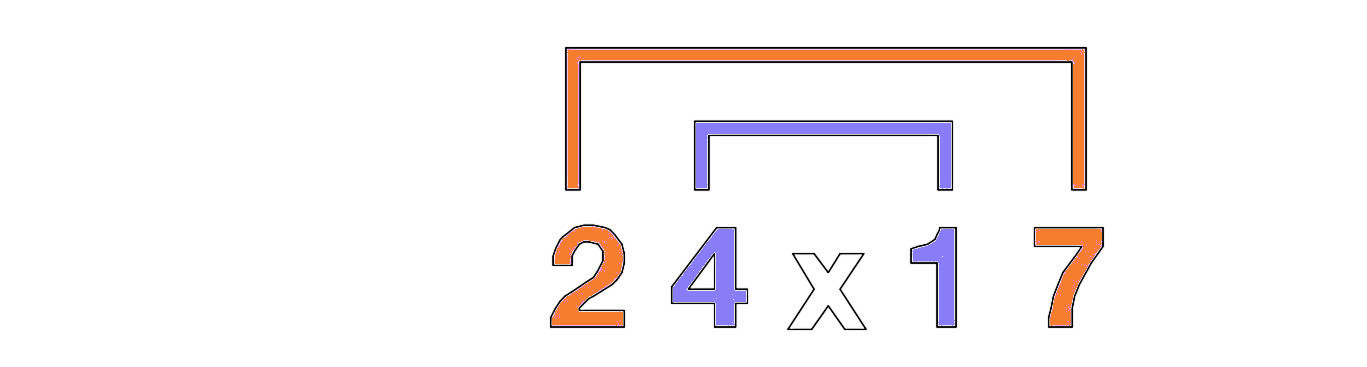
Multipliez les 2 nombres externes 2 x 7 = 14 puis les 2 nombres internes 4 x 1 = 4 et ajoutez ces 2 nombres, 14 + 4 = 18 Le résultat final sera placé dans un schéma de 4 espaces réservés. Le 18 est placé dans les deux espaces réservés du milieu.

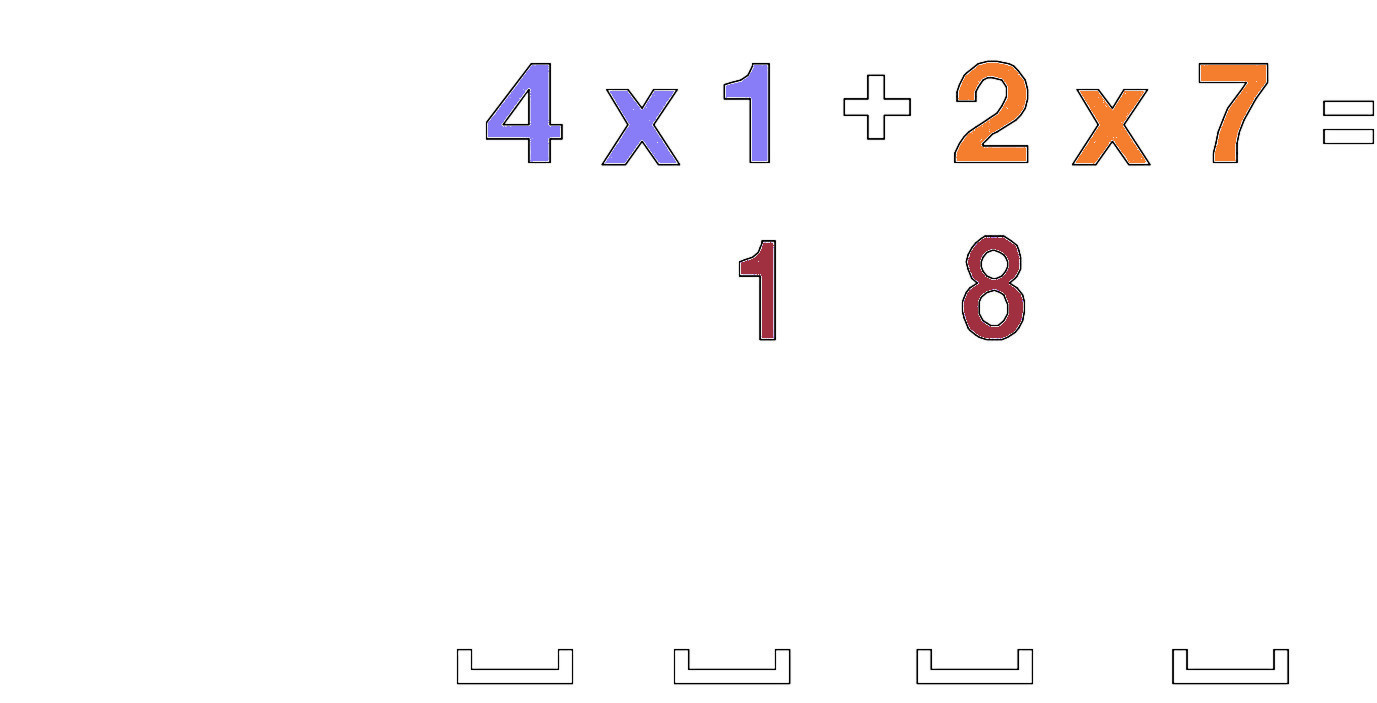
Multipliez ensuite les dizaines de chaque nombre 2 x 1 = 2 et placez-le dans les deux espaces réservés de gauche.

Multipliez ensuite les derniers chiffres de chaque nombre 4 x 7 = 28 et placez-les dans les deux espaces réservés de droite.

Maintenant, vous devez ajouter ces trois résultats de multiplication

Il faut additionner 2 + 8 = 10, nous ercritons 0 et nous transférons la 1 à la colonne suivante sur le côté gauche.

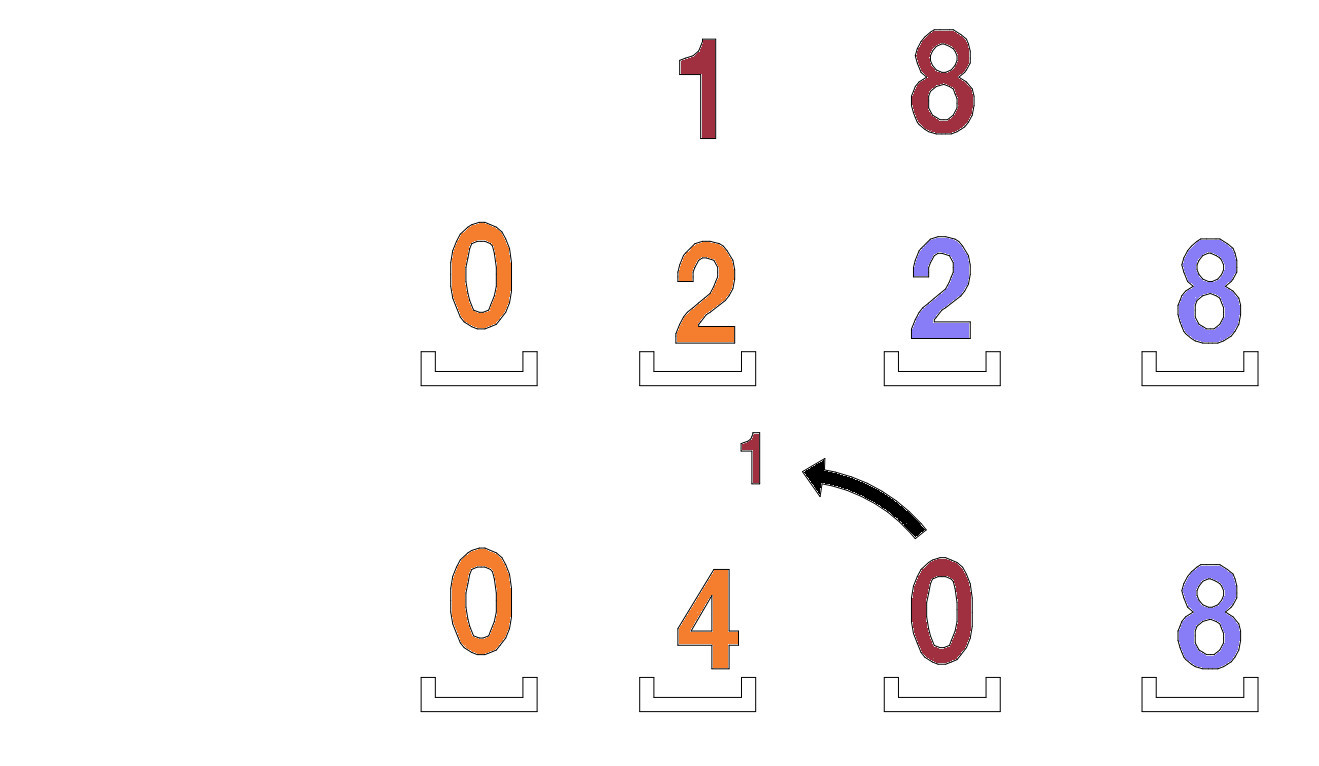
Donc, le résultat final est 24 x 17 = 408.

Pour moi, il est encore difficile de faire ces calculs dans votre tête, mais en écrivant les chiffres sur papier, c'est plus rapide que le système que j'ai appris à l'école. J'ai essayé de faire les calculs dans ma tête, mais je le trouve encore assez sujet aux erreurs, bien que de temps en temps je fasse des répétitions. Surtout, je ont tendance à oublier le portage. Pendant mon travail, néanmoins, je préfère toujours ma calculatrice HP et Excel, c'est prend juste trop d'espace mémoire dans ma tête. Je dois juste économiser mon "Système 2" pour tout le dessin travail, qui doivent être effectués simultanément aux calculs.

Entrez vos propres chiffres et appuyez sur le bouton pour voir comment le calcul est effectué.

*

Une autre méthode de multiplication, dite méthode du paysan russe

cliquez sur les flèches droite et gauche pour voir comment le calcul progresse du début à la fin

Le paragraphe suivant est extrait du livre : Valtteri Suomalainen, Marianna Wallinheimo (toim.): Sauna Syyriassa, Recallmed 1995.

Les bergers égyptiens, analphabètes et mal conseillés, font l'objet d'une attention particulière dans le commerce des ovins. Cela est dû à leur incroyable méthode de multiplication, pour ne pas dire plus. J'en ai entendu parler lorsque j'étais à Damas, mais je ne l'ai pas comprise, et franchement, je ne la comprends toujours pas. Voici ce qui se passe lors d'un échange : l'acheteur et le vendeur s'assoient sur le sable en face l'un de l'autre et tracent une croix sur le sol à l'aide d'un bâton. Après la cérémonie de marchandage propre à la culture arabe, ils finissent par se mettre d'accord sur le prix. Disons 14 agneaux pour 60 dinars chacun. Un nombre de petits cailloux égal au nombre de moutons est placé côte à côte au-dessus de la croix, et le nombre de dinars convenu est placé de l'autre côté. Si l'on doit diviser par deux le chiffre 7, par exemple, on obtient trois et demi, bien sûr, mais on ne compte pas les moitiés (on ne peut pas diviser les pierres par deux). Lorsque le côté qui diminue se retrouve inévitablement avec le chiffre un, la manœuvre la plus incroyable s'ensuit : du côté à réduire, il faut trouver toutes les piles de pierres avec un nombre pair de symboles. Comme un nombre pair est "impie", ces pierres sont simplement enlevées, y compris du côté opposé. Il suffit ensuite d'additionner les pierres du côté doublé. Comme par magie, le résultat est toujours correct. Même mon professeur de mathématiques n'a pas pu résoudre la méthode, mais il a dit qu'il y avait bien sûr une explication naturelle. J'ai essayé la méthode avec tous les nombres possibles et elle fonctionne toujours. J'ai démontré cette étrange méthode de calcul à l'aide de quelques exemples. Que celui qui peut le faire le découvre.

J'ai trouvé ce moyen sur le site suivant