Kuvittelee, että tehtaalla on tuotanto, joka pyörii ympäri vuorokauden. Tuotteet syötetään varastoon ja noudetaan varastosta. Syöttö ja nouto tulevat satunnaisesti. Koska tuotanto on ympäri vuorokauden, on syöttö varastoon vakio, mutta nouto tapahtuu vain päiväsaikaan. Koska kokonaisvaraston sisällön on pysyttävä vakiona, tämä tarkoittaa, että päivällä on suoritettava suhteellisesti enemmän noutoja. Tämä aika on sitten varastoinnin "ruuhkahetki". Päiväsaikana noutojen todennäköisyys on kaksinkertainen kuin sisäänviennin todennäköisyys. Joten voit verrata tätä noppapeliin. Kolmannes noppanumeroista on maalattu punaiseksi, ja punainen tarkoittaa sitten, että on syöttö varastoon. Loppu kaksi kolmasosaa noppen numeroista on maalattu siniseksi, ja sininen tarkoittaisi sitten, että nouto varasto tapahtuu.






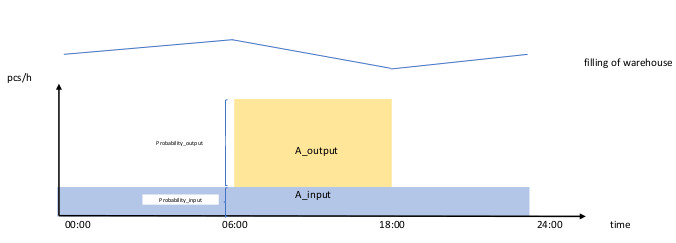
Kuvassa ylempi siksaklinja osoittaa varaston täyttöastetta. Kun linja nousee, varasto täyttyy ja kun linja laskee, varasto tyhjenee. Koska varaston täyttö tapahtuu hitaammin, kaltevuus ylöspäin on kaksi kertaa jyrkempää kuin kaltevuus alaspäin. Alemmassa kaaviossa kappale per tunti on merkitty aika-akselille. Syöttö varastoon(sininen) on jatkuvaa aika-akselia (x) pitkin, koska tehdas toimii ympäri vuorokauden. Y-akseli merkitsee varastoon menevät kappaleet tunnissa. Vaaleanpunainen alue on nouto varastosta päiväsaikaan. Joten jos varaston täyttö on oltava vakiona useimpien päivien tai viikkojen yli, Area_output-arvon (Alue nouto = noutojen määrä kpl/tunneissa kertaa 12 tunti) on oltava yhtä suuri kuin Area_input-arvo (Alue - nouto = kpl/tunneissa kertaa 24 tunti), ja se tarkoittaa, että päivän aikana ulostulon todennäköisyys (2/3) on kaksi kertaa syötön todennäköisyys (1/3).
Työntekijä voi tehdä 3 erityyppistä liikettä: 1.) vienti varastoon 2.) haku varastosta 3.) yhdistetty vienti ja haku Yhdistetty tarkoittaa: Tuotteen vienti ja heti toisen tuotteen haku jälkeen varastosta yhdellä liikkeellä. Yhdistetty jakso on nopeampaa kuin pelkästään tulon ja ulostulon lisääminen ("Tuo tuodessasi, vie mennessäsi"), koska on vähemmän liikettä. Siksi sitä pitäisi aina käyttää mikäli on mahdollista. Varaston ruuhka-ajan vähentämiseksi pitäisi yhdistää mahdollisimman paljon. Kysymys on sitten, kuinka monta vienti- ja hakuja voidaan yhdistää, jotta yhdistetyn viennin ja haun voitaisi kayttää hyväksi mahdollisimman paljon.
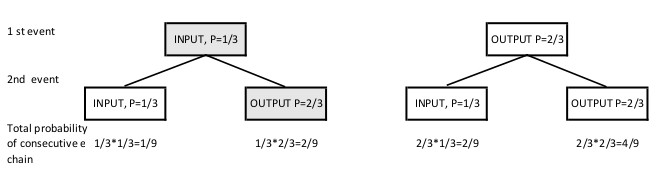
Mikä on todennäköisyys, että työntekijä voi tehdä yhdistetyn liikkeen? Alkaen yksinkertaisimmasta tapauksesta, että on vain kaksi peräkkäistä liikettä. Joten ensimmäinen liike voi olla joko tulo (todennäköisyys 1/3) tai lähtö (2/3 todennäköisyys). Ensimmäisen liikkeen jälkeen seuraavan liikkeen todennäköisyys on täsmälleen sama (1/3 vastaan 2/3) kuin aiemmin. Joten kokonaisuudessaan on 4 erilaista liikekombinaatiota, niistä jokaisella peräkkäisellä tapahtumaketjulla on erilainen todennäköisyys. Mutta kokonaisuudessa kaikki nämä todennäköisyyden ynnäävät 1/9 + 2/9+2/9 + 4/9=1 (100%). Mutta tämä ei vielä kerro mitään siitä että miten yhdistetty liike on suhteessa kokonaisuuteen eikä kerro sitä kokonaisajanvähennyksestä vielä mitään.
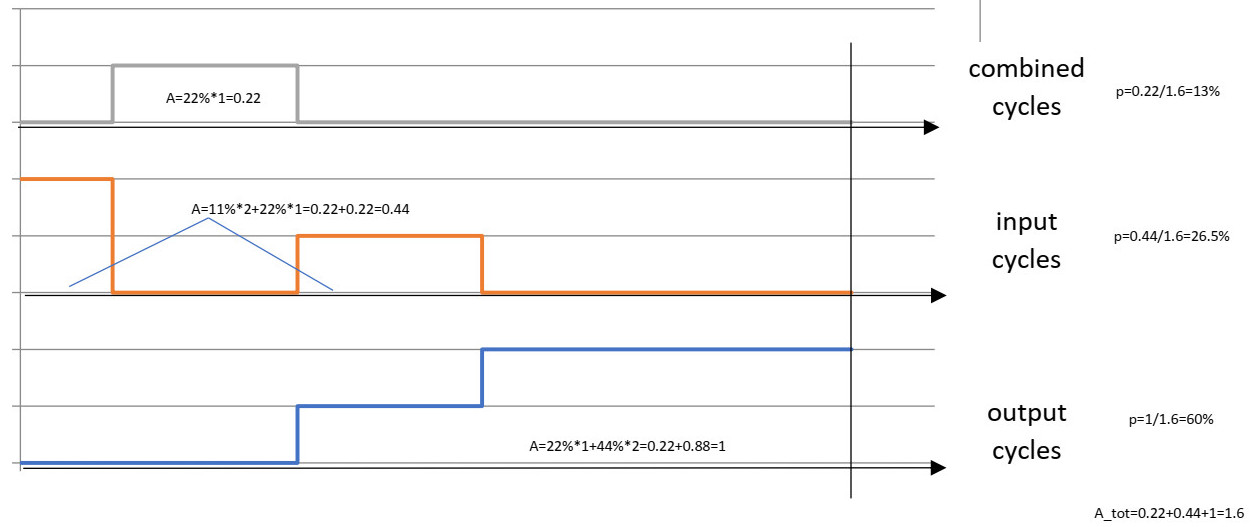
Jotta saadaan kvantitatiivisen tuloksen aikaiseksi, piirretään kaaviossa sama juttu mittakaavassa, mutta x-akseli kuvaa kunkin tapahtuman todennäköisyyden mittakaavassa. Alin sininen käyrä edustaa haku- liikkettä. Se mitä on yllä olevassa "puukaaviossa" oikean haara, on tapahtumien kulku siten, että ensimmäinen tapahtuma on nouto varastosta (p = 2/3) ja seuraavaksi haku varastosta (p = 1/3) kokonaistodennäköisyydellä 2/9 = 22%. Se tapahtuma on nyt tässä kaavassa ensimmäinen askel kahden askeleen portaikossa (askelkorkeus on 1, koska puhumme yhdestä noudosta) ja askelman leveys on 22% ja se vastaa sitä todennäkösyyttä. Ylemmän "puu kaavion" oikeanpuoleinen ulompi haara on seuraava sinisen käyrän porras, ja sen leveys on 44% (= 2/3 * 2/3 = 4/9). Ja portaan korkeus on 2, koska uloimmassa haarassa on 2 noutoja. Samoin vaaleanpunainen käyrä näyttää syöttösyklin todennäköisyyden, mutta mittakaavassa. Jyrkin osa vasemmalla puolella edustaa yllä olevan puukaavan vasen ulompaa haaraa todennäköisyydellä 1/3 * 1/3 = 1/9 (11%), joka on silloin ensimmäisen askeleen leveys vaaleanpunaisessa portaikkokäyrässä. Tämän askeleen korkeus on 2, koska se edustaa kahta syöttöliikettä peräkkäin. Keskellä on toinen "tiili", tiilen leveys 1/3 * 2/3 = 33% ja korkeus 1. Ylin harmaa käyrä edustaa yhdistelmäsyklin osan, joka on merkitty harmaalla värillä puukaaviossa. Leveys (siis vastaa todennäköisyyttä) on 1/3 * 2/3 = 2/9 = 22% ja korkeus on 1, koska meillä on vain yksi yhdistetty sykli. Jos meillä ei olisi yhdistetyn syklin "synergiavaikutusta", tämän "tiilin" korkeuden tulisi olla 2, mutta koska meillä on vain yksi tehtävä tehtävä liike, tämän lohkon korkeus on vain 1. Näiden 3 eri käyrän alapuolella oleva alue edustaa vain tietyn "nouto", "haku" tai "yhdistetty haku-nouto" tapahtuman todennäköisyyttä. Joten "nouto" käyrän alla oleva alue on 0,22 * 1 + 0,44 * 2 = 0,22 + 0,88 = 1. "Syöttö" käyrän alla oleva alue on 0,11 * 2 + 0,22 * 1 = 0,44 ja "yhdistetyn syklin" käyrän alla oleva alue on 0,22 * 1 = 0,22. Pinta-alan kaikkien kolmen käyrän alapuolella on oltava 1 (100%), koska se ei voi olla suurempi. "Nouto" - syklin todennäköisyys on lähtökäyrän alapuolella olevan alueen suhteellinen kaikkien kolmen käyrän kokonaispinta-alan kanssa. "Nouto" käyrän alla oleva pinta-ala oli 1 mutta kaikkien käyrien alla oleva pinta-ala on 0,22 + 0,44 + 1 = 1,6, joten lähtösyklin suhteellinen todennäköisyys on siis 1 / 1,6 = 0,6 (60%: n todennäköisyys "nouto"- syklistä) Vastaavasti suhde "syöttö" käyrän alla olevan alueen ja kokonaispinta-alan välissä on 0,44 / 1,6 = 0,265 (tarkoittaen 26,5%: n todennäköisyyttä syöttösyklin aikana). Ja yhdistetyn syklin todennäköisyys on 0,22/1,6 = 0,13 (13%) Kaikkien todennäköisyyksien on oltava 100% = 13,5% + 26,5% + 60% = 100%.
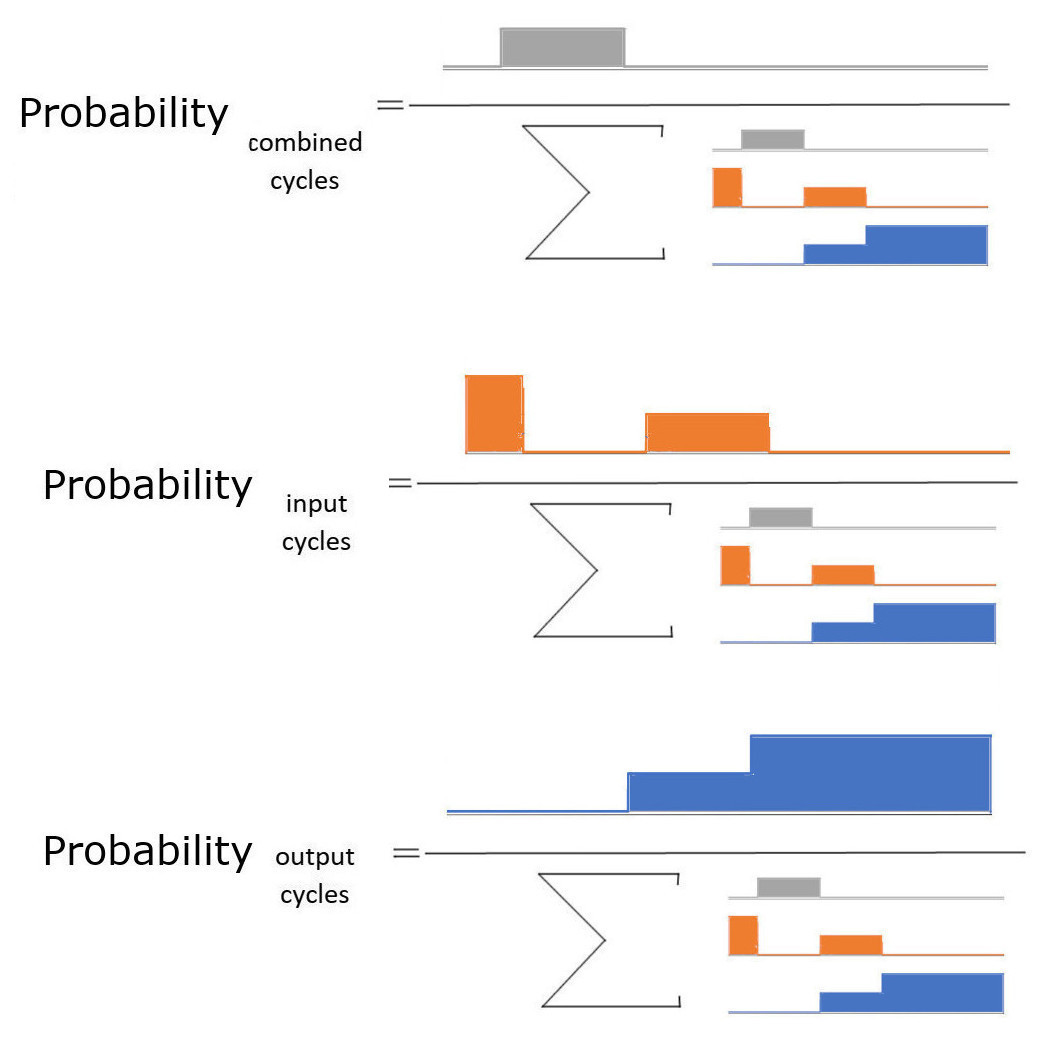
Tietyn tapahtuman (yhdistetty, syöttö, lähtö) todennäköisyys on tapahtumaan kuuluva käyrän alla oleva alue jaettuna kaikkien käyräalueiden summan kanssa.

Seuraava vaihe on lisätä yksi askel lisää, niin meillä olisi 3 peräkkäistä tapahtumaa, joko syöttö tai haku. Yhdistetty sykli ilmestyy nyt kolme kertaa ja yhteensä on kahdeksan erilaista tapahtumamahdollisuutta. Joten kun peräkkäisten tapahtumien määrä on nyt 3, mahdollisuudet ovat kaksi potenssiin kolmeen. Vastaavasti 3 peräkkäisen tulotapahtuman ketju on 1/3 * 1/3 * 1/3 = 1/27 0,037 = 3,7%, mikä ei ole kovin suuri luku.
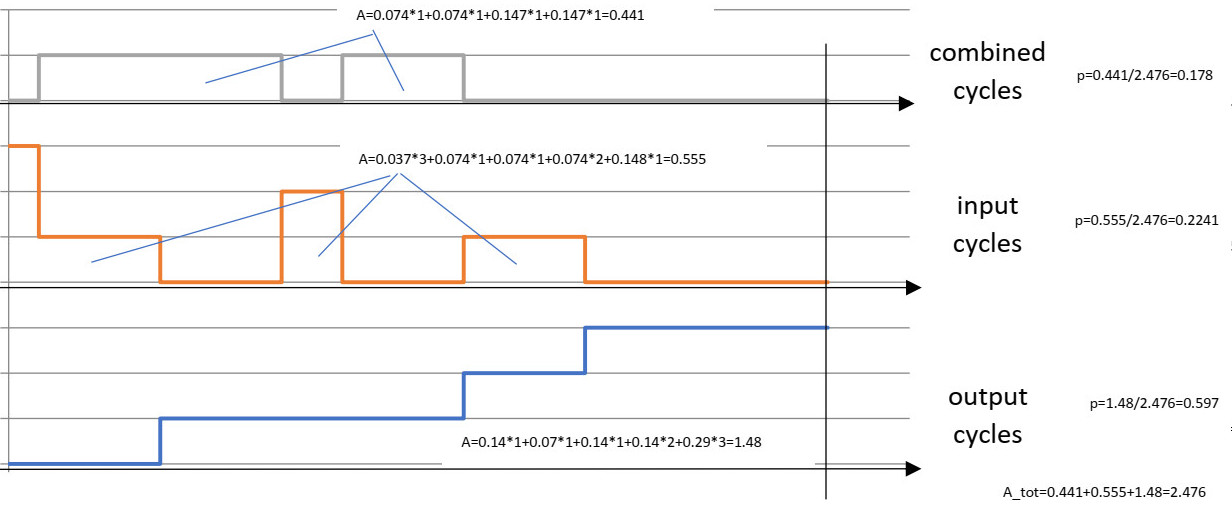
Joten kolmella peräkkäisellä tapahtumalla yhdistetyn syklin todennäköisyys on 18%, syklin todennäköisyys on 22% ja lähtösyklin todennäköisyys on 60% ja kaikkien todennäköisyyksien summa on tietenkin 100%. Voimme myös nähdä, että "portaikkokäyrämme" on saanut yhden lisä askeleen , yhteensä kolme askelta, mutta yhdistetyllä jaksokäyrällä on edelleen vain yksi askel.
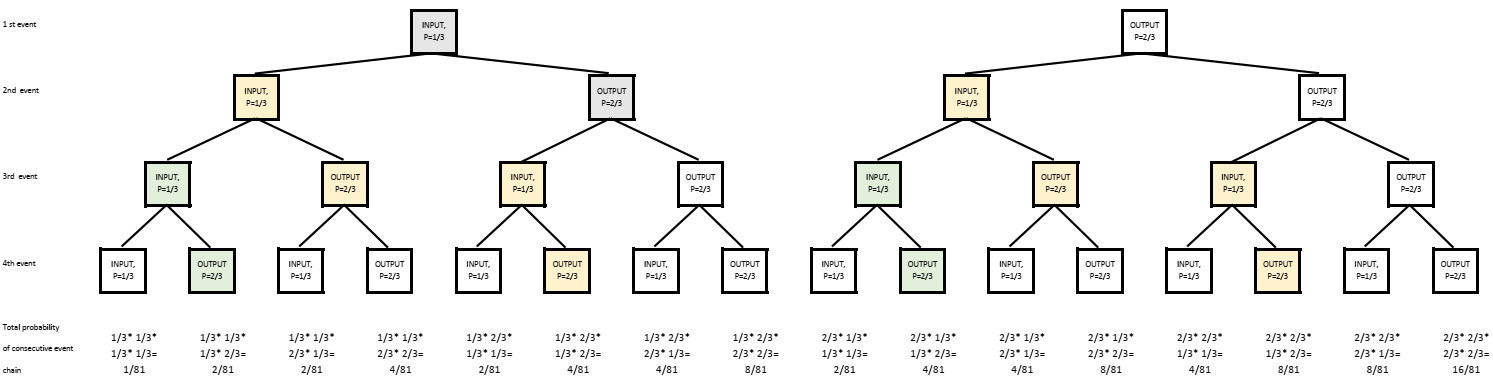
Koska olemme nyt saaneet rutiinia tähän menettelyyn ja olemme yhä uteliaampia, voimme jatkaa puukaavion laatimista jopa neljään peräkkäiseen vaiheeseen.
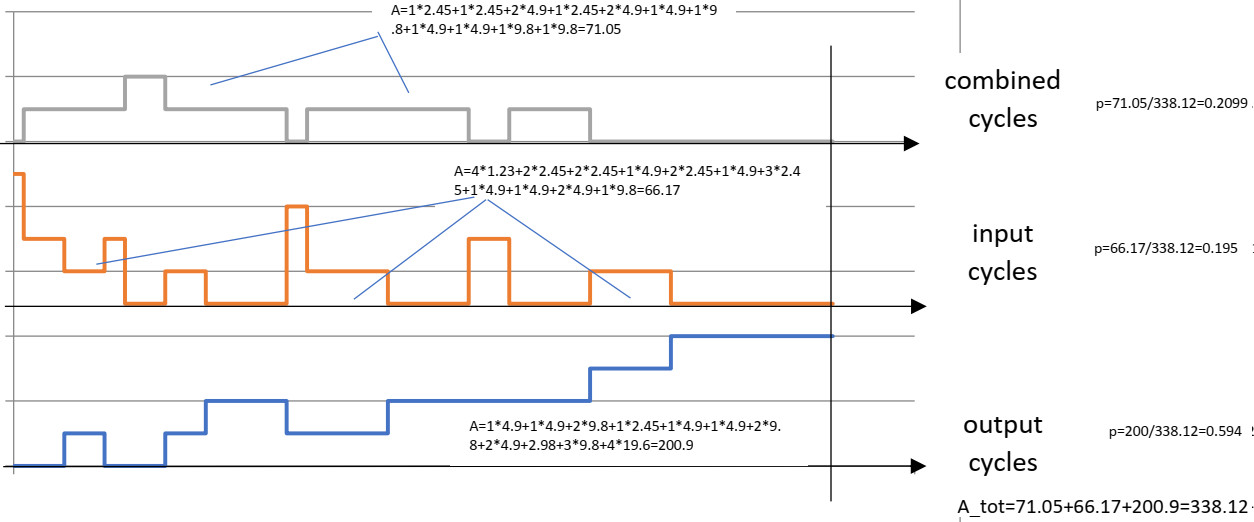
Tosiaan meillä nyt alkaa loppua nyt tilaa leveys suunnassa, näyttää siltä, että on mahdotonta sovittaa vielä enemmän oksia tähän puukaavioon. Mutta voimme edelleen jatkaa todennäköisyys kaavalla, vaikka askelleveydet ovatkin kapeammat. Mutta voimme kuitenkin saada kvantitatiivisen yleiskatsauksen siitä, kuinka monta yhdistettyä sykliä voidaan saavuttaa tulo- ja lähtöjaksoon verrattuna, koska vertaamme periaatteessa alueita kolmen eri käyrän alla.
Jatkamalla tapahtumien kasvattamista samalla kaavalla, yhdistetyn syklin todennäköisyys lähestyy 26%:a, syöttösyklin todennäköisyys on 16% ja ylitysjakson todennäköisyys on noin 58%.
Tähän asti kaikki ajatukset perustuivat oletukseen, että tehdas oli käynnissä 24 tuntia vuorokaudessa ja tuotanto oli päiväsaikaan 12 tuntia päivässä. Toinen kysymys on, kuinka tilanne näyttäisi, kun päiväaika olisi 16 tuntia, mikä vastaa päivää kolmella vuorolla, jolloin kahta vuoroa voidaan käyttää lastaamiseen. Voisiko olla mahdollista, että jos lastaus tehdään jopa 24 tuntia päivässä, kaikki syklit voitaisiin ehkä suorittaa yhdistetyssä tilassa?
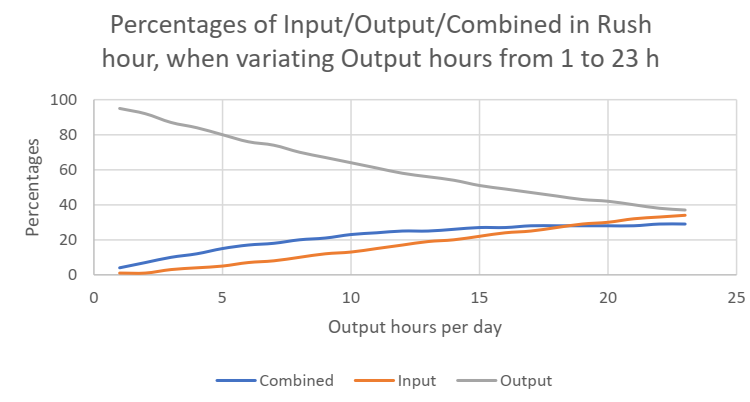
Tämä käyrä, jossa nouto aika muuttuu suhteessa syöttö- aikaan on ehkä vähän teoreettinen, koska siinä esiintyy myös sellainen epärealistinen tilanne, esimerkiksi, että päivässä on vain hyvin vähän aikaa noutamiselle (vain 1 tunti) sehän fyysisesti tarkoittaisi, että ruuhka-aikana melkein kaikki liikkeet on oltava noutoja, joten yhdistelmäsykliä eikä myöskään syöttö olisi käytännössä mahdollista. Eihän sinä ole mitään idea enää! Tämä on melko epärealistinen skenaario. Käyrän toisessa loppupäässä eri liikkeet (tulo, lähtö ja yhdistelmä) on jaettu ajallisesti tasaisesti, melkein kuin 1/3 - 1/3 - 1/3. Mutta toisin kuin odotettiin, yhdistetty syöttö- nouto sykli ei voida siis koskaan täysimääräisesti hyödyntää, selvästikin toiminnan stokastisen luonteen vuoksi, jossa ei voida ennustaa eikä hallita kumpi eri liikkeistä tulee seuraavaksi.
Yllä olevien kaavioiden laskennassa käytetty ohjelma Python-kielellä.