imaginez qu'il y a une usine, ou la production tourne 24h / 24. Les produits sont stockés. Les ordres d'entrée et de sortie entrent de façon aléatoire. L'entrée est toujours constante, mais la sortie est uniquement en plein jour. Parce que le contenu de stockage global doit rester constant, cela signifie que pendant les périodes, lorsque la sortie de la stockage est effectuée (en plein jour), relativement plus de mouvements de sortie doivent être effectués qui des cycles d'entrée. Le plein jour est alors «l'heure de pointe» du stockage, car la plupart des mouvements doivent être effectués pendant la journée. Pendant la journée, la probabilité de sortie est le double de la probabilité d'entrée. Vous pouvez donc comparer cela à un jeu de dés. Un tiers des nombres de dés est peint en rouge, et rouge signifierait alors qu'une entrée se produit. Les deux tiers des nombres de dés sont peints en bleu, et le bleu signifierait alors qu'une sortie se produit.






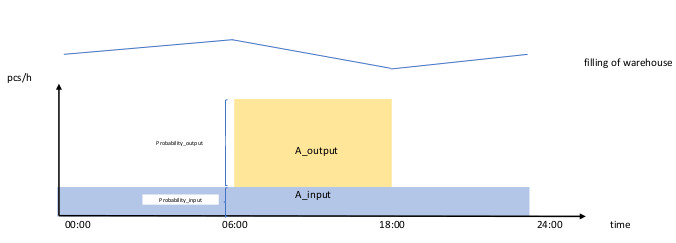
Dans l'image, la ligne supérieure en zigzag indique le remplissage du stockage. Lorsque la ligne monte, le stockage se remplit et lorsqu'il descend, le stockage est vidé. Du fait que le remplissage du stockage est plus lent, l'inclinaison vers le haut est deux fois l'inclinaison vers le bas. Dans le diagramme inférieur, le taux de remplissage en pcs per heure est marqué sur l'axe du temps. L'entrée (bleue) du stockage est continue sur l'axe du temps (x), car l'usine fonctionne 24h / 24. L'axe des y marque les pièces par heure entrant dans le stockage. La zone rouge clair est la sortie du stockage pendant la journée. Donc, si le contenu du stockage est constant sur plusieurs jours ou semaines, la Area_output doit être égale à la Area_input. et cela signifie que pendant la journée, la probabilité de sortie (2/3) est le double de la probabilité d'entrée (1/3).
Le travailleur peut effectuer 3 types de mouvements différents: 1.) cycle d'entrée 2.) cycle de sortie 3.) cycle combiné moyens combinés: saisir un article et directement après avoir sorti un article du magasin en un seul mouvement. Le cycle combiné est plus rapide qui d'ajouter simplement une entrée plus un cycle de sortie, car il y a moins de déplacements impliqués. Par conséquent, il est essentiel de considérer l'effet positif du cycle combiné sur la capacité de débit du stockage. Dans le jeu "Jetez les dés" ci-dessus, cela signifierait, "quand avons-nous un cas, qu'un numéro rouge suit un numéro bleu" et dans ce cas, ce serait une combinaison "occasion" (ou dit mieux: un gain de temps. Pour calculer la capacité de débit possible d'un stockage, les temps de cycle de tous les cycles d'entrée, de output et combinés ensemble sont pertinents. La question est alors de savoir combien de cycles d'entrée et de sortie peuvent être combinés, afin de profiter au maximum du cycle combiné.
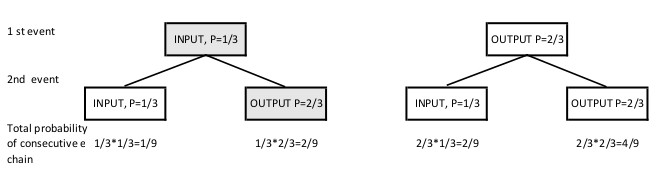
Quelle est la probabilité qu'un travailleur puisse effectuer le mouvement combiné? à partir du cas le plus simple, qu'il n'y a que deux mouvements consécutifs. Le premier mouvement peut donc être soit en entrée (probabilité 1/3) soit en sortie (probabilité 2/3). Après le premier mouvement, la probabilité du prochain mouvement est exactement la même (1/3 contre 2/3) qu'auparavant. Nous voici donc avec 4 combinaisons différentes de mouvements, et chacune de cette chaîne d'événements consécutifs a une probabilité différente. En somme, cependant, la probabilité se résume à 1/9 + 2/9 + 2/9 + 4/9 = 1. (100%). Mais ce nombre ne donne pas le cycle combiné séparément, et aussi, en n'est pas pris en compte, que le cycle combiné a réduit le nombre de pas totaux.
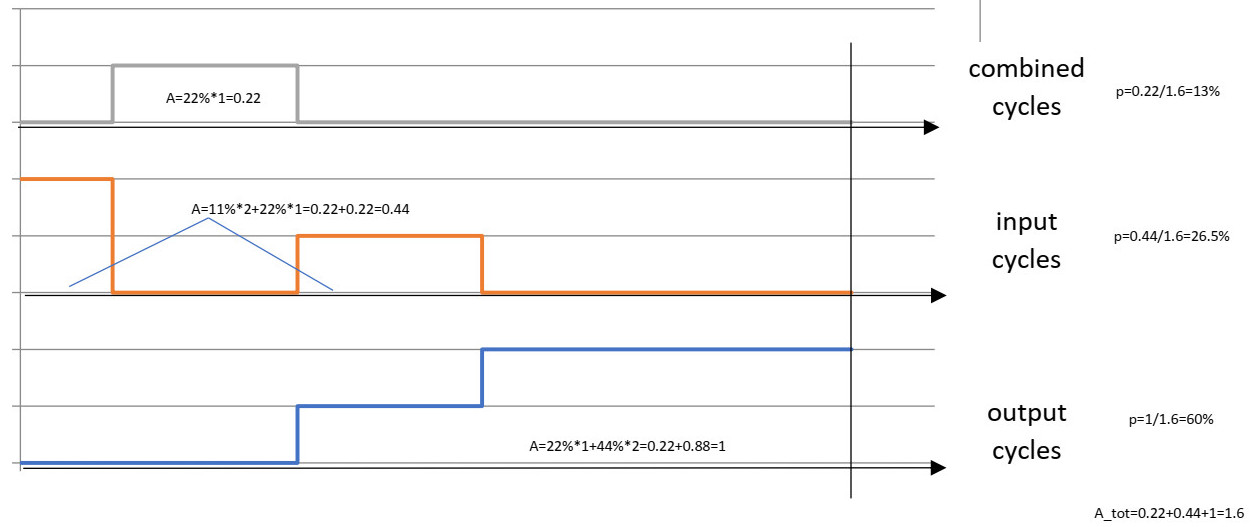
Dans le diagramme, le même fait est fait à l'échelle, mais l'axe des x est la partie de la probabilité de chaque évolution des événements qui est faite à l'échelle. La courbe bleue la plus basse représente l'échelle des mouvements de sortie. Donc, ce qui est montré sur le diagramme "arborescent" comme la branche de droite est le cours des événements avec le premier événement comme sortie (p = 2/3) et ensuite une entrée (p = 1/3) avec une probabilité totale de 2/9 = 22%, qui est maintenant la première étape (la hauteur de l'étape est 1, car nous parlons d'un événement de sortie) sur une courbe d'escalier avec deux étapes au total avec une largeur de l'étape est de 22%. La branche extérieure droite-droite de la courbe "arbre" supérieure est la prochaine étape de la courbe bleue, et elle a une largeur de 44% (= 2/3 * 2/3 = 4/9). Et la hauteur de l'étape est de 2, car nous avons 2 événements de sortie. De même, la courbe rouge montre la probabilité du cycle d'entrée, mais à l'échelle. La partie la plus raide est sur le côté gauche, et elle représente la branche externe gauche de diagramme d'arbre ci-dessus, avec une probabilité de 1/3 * 1/3 = 1/9 (11%), qui est alors la largeur de la première étape de la courbe d'escalier rouge clair descendant. La hauteur de cette étape est de 2 car il s'agit de deux mouvements d'entrée ensemble. Au milieu se trouve une autre brique, avec une largeur de 1/3 * 2/3 = 33% et la hauteur de 1. La courbe grise supérieure montre la partie du cycle combiné, qui est marquée en gris dans le diagramme d'arbre. La largeur (synonyme de probabilité) est 1/3 * 2/3 = 2/9 = 22% et la hauteur est 1, car nous n'avons qu'un seul événement. Si nous n'avions pas l'effet "synergie" du cycle combiné, la hauteur de ce bloc devrait être de 2, mais comme nous n'avons qu'un seul mouvement à faire, la hauteur de ce bloc n'est que de 1. L'aire sous chacune de ces 3 courbes différentes représente la probabilité de l'événement respectif. L'aire sous la courbe du cycle de sortie est donc de 0,22 * 1 + 0,44 * 2 = 0,22 + 0,88 = 1. L'aire sous la courbe d'entrée est de 0,11 * 2 + 0,22 * 1 = 0,44 et l'aire sous la courbe de cycle combiné est de 0,22 * 1 = 0,22. L'aire sous les trois courbes ensemble doit être de 1 (100%) car elle ne peut pas être plus. Et la probabilité du cycle de sortie est le quotient de l'aire sous la courbe de sortie avec l'aire totale sous les trois courbes. Ainsi, l'aire sous la courbe de sortie était 1 et l'aire sous toutes les courbes ensemble est 0,22 + 0,44 + 1 = 1,6, donc la probabilité relative du cycle de sortie est donc 1 / 1,6 = 0,6 (probabilité de 60% du cycle de sortie) Respectivement, la relation de l'aire sous la courbe d'entrée à l'aire totale est de 0,44 / 1,6 = 0,265 (soit une probabilité de 26,5% pour le cycle d'entrée) Et la probabilité du cycle combiné est de 0,2271,6 = 0,13 (13%) Au total, toutes les probabilités doivent totaliser 100% = 13,5% + 26,5% + 60% = 100%.
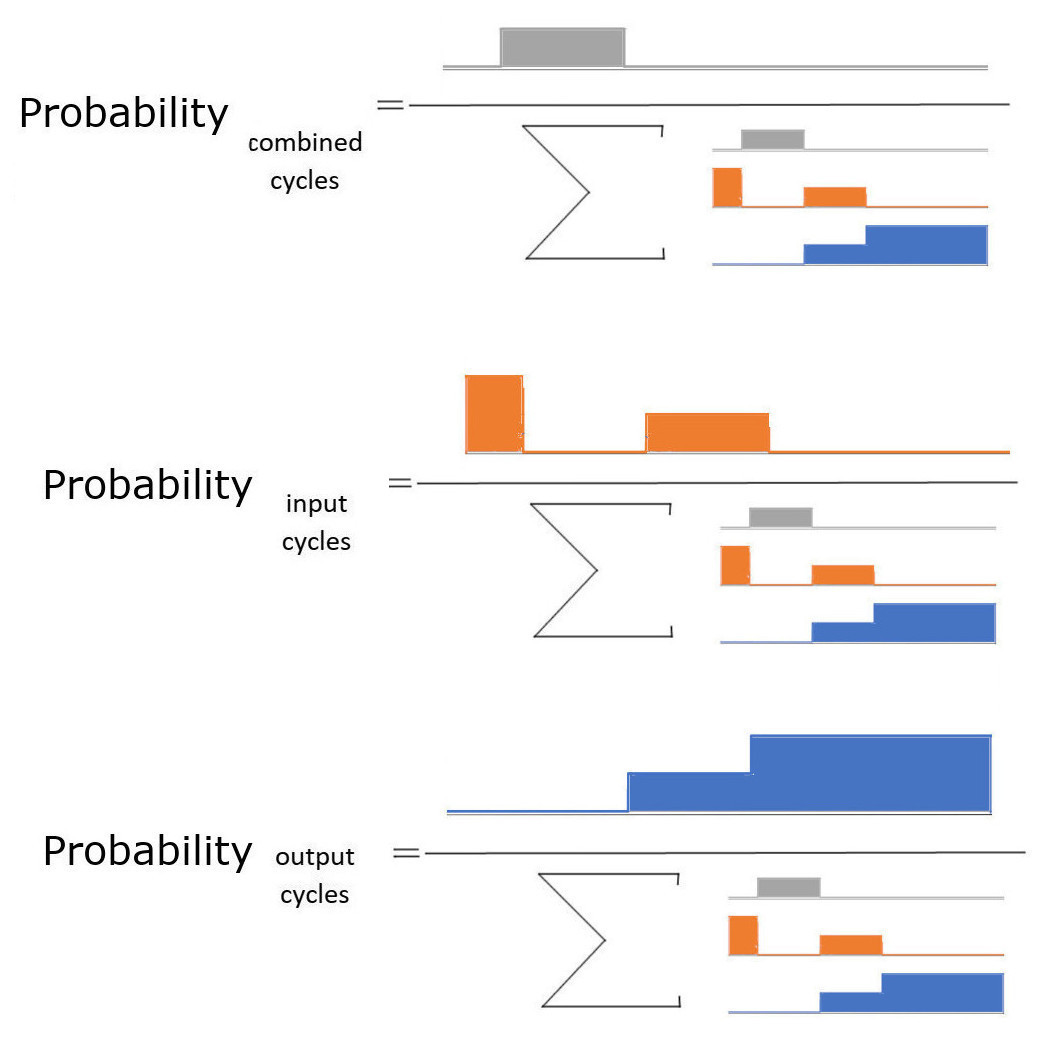
La probabilité des différents événements (combinés, entrées, sorties) est la zone de l'événement respectif divisé par la zone de tous les événements ensemble.

La prochaine étape de l'examen consiste à ajouter une étape de plus, nous aurions donc 3 événements consécutifs. Le cycle combiné apparaît désormais trois fois dans un total de huit possibilités d'événements différentes. Donc, en fonction du nombre d'événements consécutifs, les possibilités sont toujours de 2 à la puissance du montant de l'événement. Respectivement, la chaîne de 3 événements d'entrée consécutifs est 1/3 * 1/3 * 1/3 = 1/27 0,037 = 3,7%, ce qui n'est pas un nombre élevé.
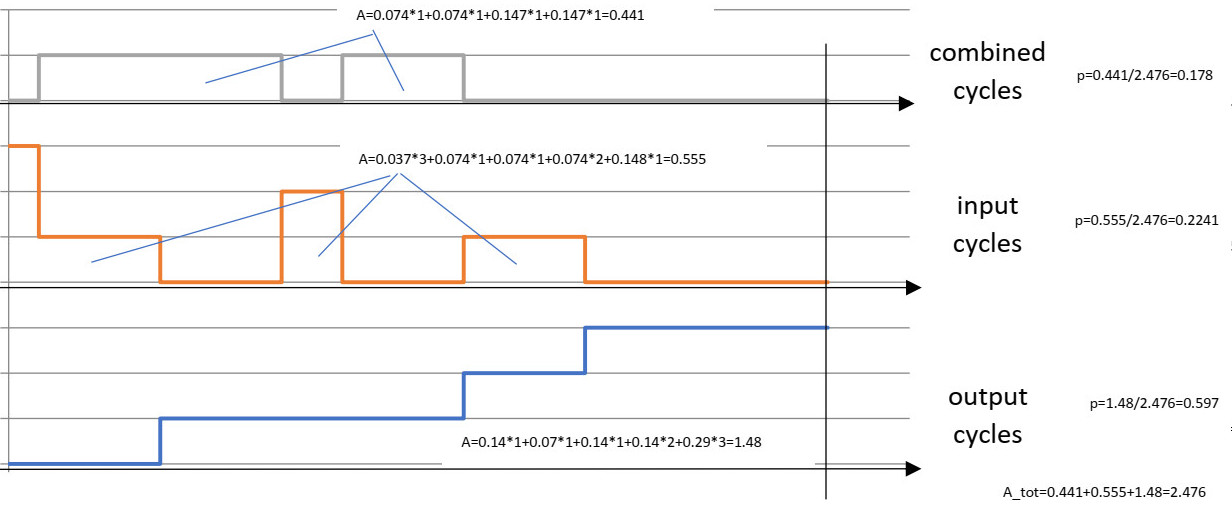
Ainsi, avec 3 événements consécutifs, la probabilité de cycle combiné est de 18%, la probabilité de cycle d'entrée est de 22% et la probabilité de cycle de sortie est de 60% et la somme de toutes les probabilités est bien sûr de 100%. Nous pouvons également voir que notre "courbe d'escalier" a une étape de plus, trois étapes au total, mais la courbe de cycle combiné n'a qu'une seule étape.
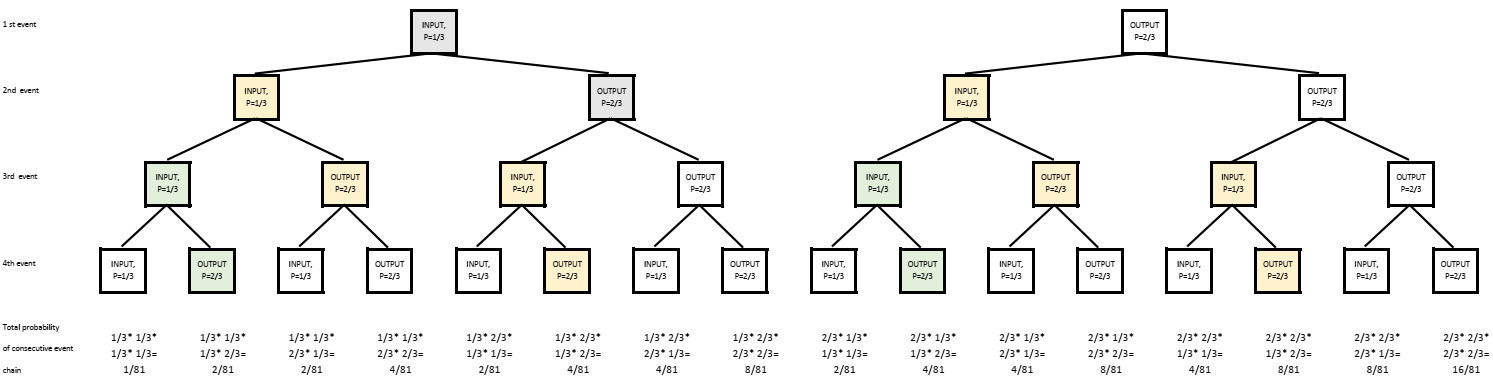
Comme nous avons maintenant une routine avec cette procédure et que nous devenons de plus en plus curieux, nous pouvons continuer à faire le diagramme d'arbre en quatre étapes consécutives.
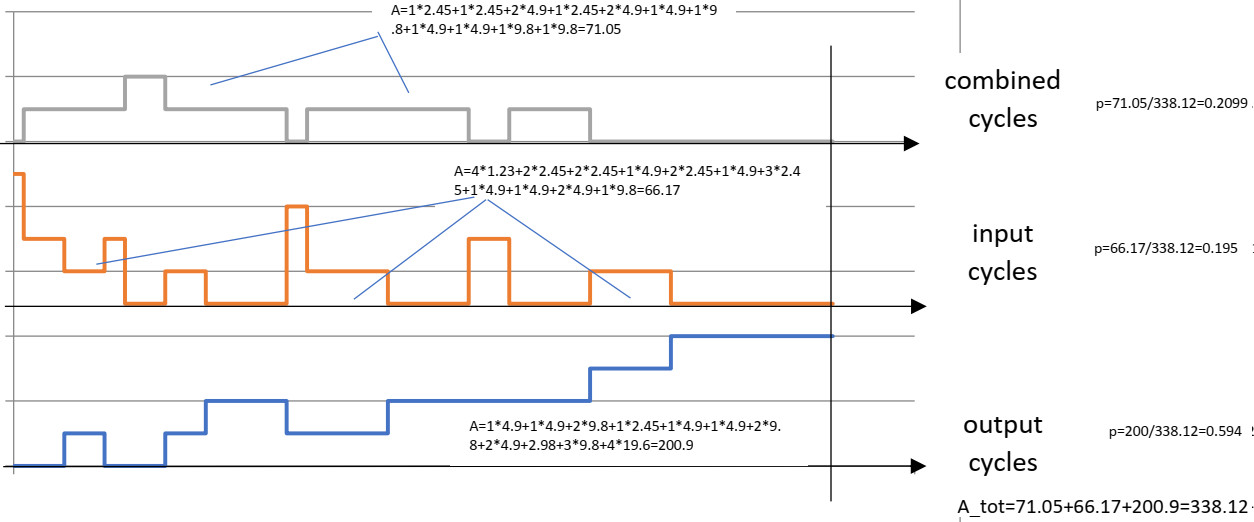
En fait, maintenant que nous avons des problèmes d'espace dans le sens de la largeur du papier, il semble impossible d'intégrer encore plus de branches dans cet arbre. Mais nous pouvons toujours continuer avec le schéma de probabilité, bien que les largeurs de pas deviennent de plus en plus étroites. Mais nous pouvons néanmoins obtenir un aperçu quantitatif du nombre de cycles combinés pouvant être réalisés par rapport au cycle d'entrée et de sortie, car nous comparons essentiellement des zones sous les trois courbes différentes.
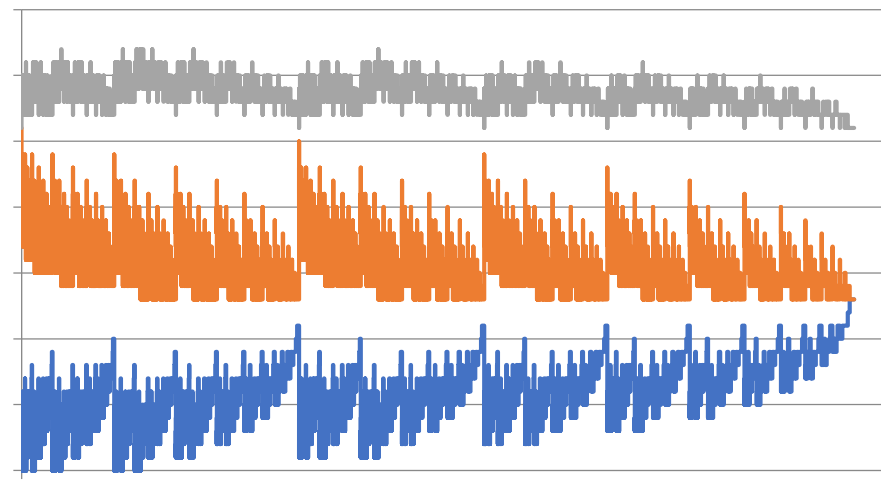
NA
Jusqu'à présent, toutes les pensées étaient basées sur l'hypothèse, que l'usine fonctionnait 24h / 24h et la sortie était de jour 12 heures par jour. Une autre question est de savoir à quoi ressemblerait la situation lorsque la journée serait de 16 heures, ce qui correspondrait à une journée avec trois équipes, où deux équipes peuvent être utilisées pour les activités de chargement. Serait-il possible, que, si le chargement est effectué même 24 heures par jour, tous les cycles puissent être effectués en mode combiné?
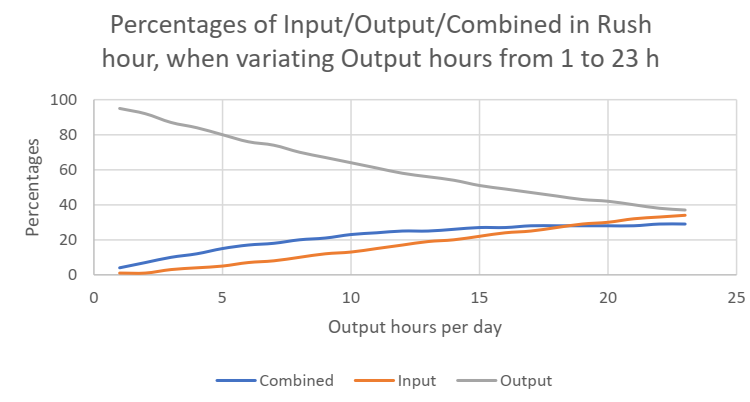
Cette courbe, où le temps de sortie pendant la journée est variable, est un peu théorique, car elle montre également une situation irréaliste, que, par exemple, quand il n'y a que très peu d'heures de sortie par jour (disons 1h seulement) en termes, que pendant l'heure de pointe, presque tous les mouvements doivent être des mouvements de sortie, donc aucune combinaison n'est possible et l'entrée n'est pas possible. Mais c'est un scénario plutôt irréaliste. À l'autre extrémité de la courbe, les proportions des différents mouvements (entrée, sortie et combinés) sont assez uniformes, presque comme 1/3 - 1/3 - 1/3. Mais, contrairement aux attentes, le cycle combiné ne peut jamais être complètement exploité, évidemment en raison de la nature stochastique du processus, où il est impossible de prédire ou de contrôler lequel des différents mouvements se produira ensuite.
Pour calculer les diagrammes ci-dessus, un programme en la langage Python